InverseRadon

InverseRadon[image]

gives the inverse discrete Radon transform of image.

InverseRadon[image,{w,h}]

specifies the width w and the height h of the resulting image.

Details and Options

  • InverseRadon finds an approximation of the inverse of the Radon transform, using a filtered back projection method.
  • InverseRadon operates on an image that represents a discrete Radon transform of an image, assuming that the columns represent angles from 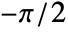to 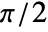relative to the vertical axis, and the rows represent scaled distances to the center of the output.
  • InverseRadon[image] returns a square image whose sides have the same length as the diagonal of image.
  • InverseRadon[image,w] is equivalent to InverseRadon[image,{w,w}].
  • By default, InverseRadon[image,…] computes one back projection for each column in image. InverseRadon[image,{w,h},n] uses n back projections.
  • InverseRadon takes a Method option that specifies a frequency filter to be applied before computing the back projection. The domain of the filter is scaled to be 0 to 1. By default, a Hann filter is used.
  • Typical filter settings include:
  • #&ramp filter with constant slope
    #Cos[#Pi]&ramp filter multiplied by cosine function
    (1+Cos[#Pi])/2&Hann filter (default)
    (.54+.46Cos[#Pi])&Hamming filter
    Sqrt[1/(1+#^(2n))]&Butterworth filter of order n
    Noneno filtering
  • With Method->{filter,"CutoffFrequency"->f}, frequency values greater than f are set to zero. By default, no cutoff is applied.

Examples

open allclose all

Basic Examples  (1)

Inverse Radon transform of a sinogram:

Scope  (2)

Reconstruct an image of a specific size:

Specify the number of back projections:

Options  (2)

Method  (2)

By default, a Hann filter is applied before computing the back projection:

Use a ramp filter with constant slope:

Use no filter:

By default, no cutoff is used:

Use a cutoff frequency to get a smoother image:

Applications  (1)

Reconstruct line segments from the result of a Radon transform:

Properties & Relations  (2)

Compute the inverse of the Radon transform:

Inverse Radon transform of a horizontal line:

Wolfram Research (2010), InverseRadon, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseRadon.html (updated 2014).

Text

Wolfram Research (2010), InverseRadon, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseRadon.html (updated 2014).

CMS

Wolfram Language. 2010. "InverseRadon." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/InverseRadon.html.

APA

Wolfram Language. (2010). InverseRadon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseRadon.html

BibTeX

@misc{reference.wolfram_2024_inverseradon, author="Wolfram Research", title="{InverseRadon}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/InverseRadon.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inverseradon, organization={Wolfram Research}, title={InverseRadon}, year={2014}, url={https://reference.wolfram.com/language/ref/InverseRadon.html}, note=[Accessed: 21-November-2024 ]}