Radon

Radon[image]

gives an image representing the discrete Radon transform of image.

Radon[image,{w,h}]

specifies the width w and the height h of the resulting image.

Radon[image,{w,h},{θ1,θ2}]

computes the Radon transform only for angles from θ1 to θ2.

Details and Options

  • Radon[image] computes the Radon transform of image and returns the result as an image in which each pixel value gives a measure for the presence of a line in image.
  • By default, Radon uses a normal line parametrization 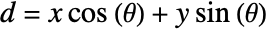, where 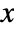and 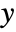are image coordinates, 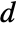is the distance between the origin of the image coordinate system and the line, and 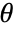is the angle between the normal and the horizontal axis.
  • Angles are given in radians. An angle 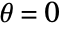in the image corresponds to a vertical line.
  • In the image returned by Radon[image], the columns represent angles in the range 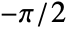to 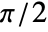, and the rows represent pixel distances in the range 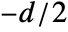to 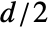, where 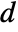is the length of the diagonal of image.
  • The height of the image returned by Radon[image] is equal to the length of the diagonal of image. The width is chosen so that the image and its Radon transform have approximately the same resolution.
  • Radon returns an image in which values are normalized so that the highest possible value is 1.
  • Radon[image,{w,h},{θ1,θ2}] computes the Radon transform for angles in the range θ1 to θ2.
  • Radon[image,{w,h},{θ1,θ2},{x0,y0}] uses {x0,y0} as the origin of the image coordinate system. By default, {x0,y0} is set to be the center of the image.
  • The origin {x0,y0} is specified in the standard image coordinate system where 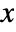runs from 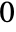to width and 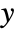runs from 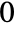to height. Position {0,0} corresponds to the bottom-left corner of the image.
  • Radon[image,{w,h},{θ1,θ2},{x0,y0},{d1,d2}] uses a line parametrization with {x,y} as the origin of normal vectors and distances running in the range from d1 to d2.
  • Radon works with binary, grayscale, and other images.
  • Radon operates separately on each channel in an image.
  • Radon[image,…,Method->method] specifies the method to use to compute the Radon transform.
  • With the default setting Method->"Radon", Radon computes for each pixel of the resulting image the sum of the pixels along the corresponding line in the input image, divided by the number of pixels on the diagonal. Radon uses bilinear subpixel interpolation.     
  • With Method->"Hough", the standard Hough transform is computed. For each pixel in the input image, a value is accumulated in each column of the resulting image. The Hough transform iterates over the pixels in the input image, accumulating the intensity value at the corresponding point in each column of the output image.

Examples

open allclose all

Basic Examples  (3)

Radon transform of a CT image of a head:

Radon transform of a grayscale image:

Radon transform of a color image:

Scope  (2)

The Radon transform of an image with rectangular objects:

The Radon transform of the perimeters of rectangles shows pairs of peaks:

Options  (3)

Method  (3)

Compute the standard Hough transform:

Standard Hough transform is typically fast, but it also includes some artifacts:

Radon transform gives a more accurate result:

Applications  (1)

Radon transform of a color image:

Use segmentation by color to locate the maxima:

Properties & Relations  (1)

Radon transform of a white disk:

Possible Issues  (1)

Computing the Radon transform of a noisy image shows the sinusoidal parameter range of the transformed image:

Interactive Examples  (1)

Radon transform of an arbitrary line:

Wolfram Research (2010), Radon, Wolfram Language function, https://reference.wolfram.com/language/ref/Radon.html.

Text

Wolfram Research (2010), Radon, Wolfram Language function, https://reference.wolfram.com/language/ref/Radon.html.

CMS

Wolfram Language. 2010. "Radon." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Radon.html.

APA

Wolfram Language. (2010). Radon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Radon.html

BibTeX

@misc{reference.wolfram_2024_radon, author="Wolfram Research", title="{Radon}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/Radon.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_radon, organization={Wolfram Research}, title={Radon}, year={2010}, url={https://reference.wolfram.com/language/ref/Radon.html}, note=[Accessed: 30-December-2024 ]}