JacobiAmplitude
JacobiAmplitude[u,m]
ヤコビの楕円関数の振幅![]() を与える.
を与える.
詳細

- 記号操作・数値操作の両方に適した数学関数である.
- JacobiAmplitude[u,m]は,楕円関数の引数 u を振幅関数 ϕ に変換する.
- JacobiAmplitudeは,第1種楕円積分の逆となる.
![u=TemplateBox[{phi, m}, EllipticF] u=TemplateBox[{phi, m}, EllipticF]](Files/JacobiAmplitude.ja/2.png) であれば,
であれば,![phi=TemplateBox[{u, m}, JacobiAmplitude] phi=TemplateBox[{u, m}, JacobiAmplitude]](Files/JacobiAmplitude.ja/3.png) となる.
となる. - JacobiAmplitude[u,m]は,
![2 s TemplateBox[{m}, EllipticK]+ⅈ (4 t+1) TemplateBox[{{1, -, m}}, EllipticK] 2 s TemplateBox[{m}, EllipticK]+ⅈ (4 t+1) TemplateBox[{{1, -, m}}, EllipticK]](Files/JacobiAmplitude.ja/4.png) から
から![2 s TemplateBox[{m}, EllipticK]+ⅈ (4 t+3) TemplateBox[{{1, -, m}}, EllipticK] 2 s TemplateBox[{m}, EllipticK]+ⅈ (4 t+3) TemplateBox[{{1, -, m}}, EllipticK]](Files/JacobiAmplitude.ja/5.png) までの複素 u 平面に,整数
までの複素 u 平面に,整数 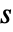 と
と 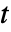 のすべてのペアについて不連続な分枝切断線を持つ.
のすべてのペアについて不連続な分枝切断線を持つ. - 特別な引数の場合,JacobiAmplitudeは,自動的に厳密値を計算する.
- JacobiAmplitudeは任意の数値精度で評価できる.
- JacobiAmplitudeは自動的にリストに縫い込まれる.
例題
すべて開くすべて閉じるスコープ (26)
数値評価 (5)
JacobiAmplitudeを高精度で効率よく評価する:
Aroundを使って平均的な場合の統計区間を計算する:
MatrixFunctionを使って行列のJacobiAmplitude関数を計算することもできる:
可視化 (3)
JacobiAmplitude関数をパラメータ ![]() のさまざまな値についてプロットする:
のさまざまな値についてプロットする:
JacobiAmplitudeをパラメータ ![]() の関数としてプロットする:
の関数としてプロットする:
関数の特性 (5)
級数展開 (3)
JacobiAmplitudeはベキ級数に適用できる:
関数表現 (3)
アプリケーション (4)
一般化されたフーリエ(Fourier)級数を形成しプロットする:
楕円パラメータ ![]() と
と ![]() となるようなトリプレッツ
となるようなトリプレッツ![]() からの球面三角形:
からの球面三角形:
球面三角形のすべての角度と辺の測定値を関連付けるCagnoliの方程式を検証する:
リュイリエ(L'Huilier)の定理を使って過剰を計算する[MathWorld]:
特性と関係 (5)
PowerExpandを使って逆関数の多価性を無視する:
三角関数をJacobiAmplitudeに適用する:
JacobiAmplitudeは,任意の整数 ![]() と
と ![]() について,
について,![]() から
から![]() までの分枝切断線を持つ:
までの分枝切断線を持つ:
テキスト
Wolfram Research (1988), JacobiAmplitude, Wolfram言語関数, https://reference.wolfram.com/language/ref/JacobiAmplitude.html (2020年に更新).
CMS
Wolfram Language. 1988. "JacobiAmplitude." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/JacobiAmplitude.html.
APA
Wolfram Language. (1988). JacobiAmplitude. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JacobiAmplitude.html