JordanModelDecomposition

JordanModelDecomposition[ssm]

给出状态空间模型 ssm 的约旦分解.

更多信息

  • 结果是列表 {p,jc}，其中 p 是相似度矩阵，而 jc 是 ssm 的约旦标准型.
  • 状态空间模型 ssm 可以以 StateSpaceModel[{a,b,c,d}] 的形式给出，其中 a、b、c 和 d 表示在一个连续时间系统或者离散时间系统中的状态、输入、输出和传递矩阵：
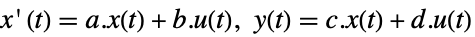
  • 连续时间系统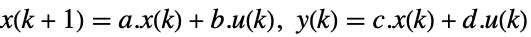
    离散时间系统
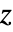  • 变换公式 把系统转化为约旦标准型，其中 是新的状态向量，而 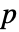是由 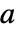的线性独立的特征向量所生成的相似矩阵：
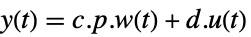
  • w'(t)=TemplateBox[{p}, Inverse].a.p.w(t)+TemplateBox[{p}, Inverse].b.u(t), 连续时间系统
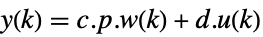    w(k+1)=TemplateBox[{p}, Inverse].a.p.w(k)+TemplateBox[{p}, Inverse].b.u(k),.离散时间系统
  • 新的状态矩阵 TemplateBox[{p}, Inverse].a.p 是旧的状态矩阵 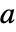的约旦标准型.

范例

打开所有单元关闭所有单元

基本范例  (1)

计算状态空间模型的约旦分解：

范围  (4)

二阶系统的约旦分解：

离散时间系统的约旦分解：

在二阶块中给出复数极点的变换：

在约旦块中重复出现的极点：

应用  (2)

当且仅当 的约旦块含有不同的特征值，并且对应于每个约旦块的最后一行的 的行元素不全是0，则称该系统是可控制的：

当且仅当 的约旦块含有不同的特征值，并且对应于每个约旦块的 的列元素不全是0，则称该系统是可观察的：

属性和关系  (3)

在约旦标准型中，特征值位于状态矩阵的对角线上：

该约旦标准型通过相似变换与原系统相关：

一个状态空间模型的约旦标准型是与它的状态矩阵的约旦分解相关联的相似变换：

可能存在的问题  (1)

JordanModelDecomposition 不支持描述器系统：

使用 KroneckerModelDecomposition 来分隔系统的模式：

Wolfram Research (2010)，JordanModelDecomposition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

文本

Wolfram Research (2010)，JordanModelDecomposition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

CMS

Wolfram 语言. 2010. "JordanModelDecomposition." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

APA

Wolfram 语言. (2010). JordanModelDecomposition. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/JordanModelDecomposition.html 年

BibTeX

@misc{reference.wolfram_2024_jordanmodeldecomposition, author="Wolfram Research", title="{JordanModelDecomposition}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_jordanmodeldecomposition, organization={Wolfram Research}, title={JordanModelDecomposition}, year={2010}, url={https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}, note=[Accessed: 21-November-2024 ]}