JuliaSetIterationCount

JuliaSetIterationCount[f,z,p]

returns the number of iterations, beginning with the complex number , of the function needed to determine whether p is in the Julia set of f.

JuliaSetIterationCount[c,p]

returns the number of iterations, beginning with the complex number , of the function needed to determine whether p is in the Julia set of .

JuliaSetIterationCount[f,z,{p1,p2,…}]

returns a list of the number of iterations required to determine whether each member of {p1,p2,…} is in the Julia set of f.

JuliaSetIterationCount[c,{p1,p2,…}]

returns a list of the number of iterations required to determine whether each member of {p1,p2,…} is in the Julia set of .

Details and Options

  • The Julia set of a function f is the closure of the set of all repelling fixed points of f.
  • JuliaSetIterationCount uses the same "OrbitDetection" algorithm as JuliaSetPlot.
  • With MaxIterations->n, where n is a positive integer, the function 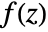will be iterated at most n times to determine if z lies outside of the Julia set. If z is not found to lie outside the Julia set, JuliaSetIterationCount returns n+1. The default setting is MaxIterations->1000.
  • With WorkingPrecision->n, each iteration is internally calculated to n digits of precision. Without this option, the amount of precision used is determined based on the precision of p and the value of MaxIterations.

Examples

open allclose all

Basic Examples  (2)

Four iterations are needed to determine that is not in the Julia set of :

Calculate the iterations for a list of numbers:

Scope  (6)

Find the iteration count of for the Julia set of where :

Find the iteration count of 0 for the Julia set of a polynomial:

Find the iteration count of 0 for the Julia set of a rational function:

Find the iteration counts for a list of numbers:

Find the iteration counts for an array of numbers:

JuliaSetIterationCount works on all kinds of numbers:

Options  (2)

MaxIterations  (1)

MaxIterations must be increased if the number of iterations needed exceeds 1000:

WorkingPrecision  (1)

Increasing WorkingPrecision can increase accuracy, at the cost of more time:

Setting WorkingPrecision too low can result in the iteration entering a false loop:

Properties & Relations  (3)

ArrayPlot applied to JuliaSetIterationCount[c] is essentially JuliaSetPlot[c]:

The red dot in the middle comes from taking the Log after JuliaSetIterationCount returns 0:

JuliaSetIterationCount can accept lists, which is faster than applying it to each member of a list:

Possible Issues  (1)

The precision of a point may affect the result:

Neat Examples  (2)

Display the iteration count as height:

Create a three-dimensional image by varying a parameter:

Wolfram Research (2014), JuliaSetIterationCount, Wolfram Language function, https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html.

Text

Wolfram Research (2014), JuliaSetIterationCount, Wolfram Language function, https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html.

CMS

Wolfram Language. 2014. "JuliaSetIterationCount." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html.

APA

Wolfram Language. (2014). JuliaSetIterationCount. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html

BibTeX

@misc{reference.wolfram_2024_juliasetiterationcount, author="Wolfram Research", title="{JuliaSetIterationCount}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_juliasetiterationcount, organization={Wolfram Research}, title={JuliaSetIterationCount}, year={2014}, url={https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html}, note=[Accessed: 21-December-2024 ]}