WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

JuliaSetIterationCount[f,z,p]

p が f のジュリア集合に含まれるかどうかを求めるために必要な関数 の反復回数を，複素数 から始めて返す．

JuliaSetIterationCount[c,p]

p が のジュリア集合に含まれるかどうかを求めるために必要な関数 の反復回数を，複素数 から始めて返す．

JuliaSetIterationCount[f,z,{p1,p2,…}]

{p1,p2,…}の各要素が f のジュリア集合に含まれるかどうかを求めるのに必要な，反復回数のリストを返す．

JuliaSetIterationCount[c,{p1,p2,…}]

{p1,p2,…}の各要素が のジュリア集合に含まれるかどうかを求めるのに必要な，反復回数のリストを返す．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
オプション  
MaxIterations  
WorkingPrecision  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
関連するガイド
履歴
引用書式

JuliaSetIterationCount

JuliaSetIterationCount[f,z,p]

p が f のジュリア集合に含まれるかどうかを求めるために必要な関数 の反復回数を，複素数 から始めて返す．

JuliaSetIterationCount[c,p]

p が のジュリア集合に含まれるかどうかを求めるために必要な関数 の反復回数を，複素数 から始めて返す．

JuliaSetIterationCount[f,z,{p1,p2,…}]

{p1,p2,…}の各要素が f のジュリア集合に含まれるかどうかを求めるのに必要な，反復回数のリストを返す．

JuliaSetIterationCount[c,{p1,p2,…}]

{p1,p2,…}の各要素が のジュリア集合に含まれるかどうかを求めるのに必要な，反復回数のリストを返す．

詳細とオプション

  • 関数 f のジュリア集合は，f のすべての反発固定点の集合の閉包である．
  • JuliaSetIterationCountは，JuliaSetPlotと等しい"OrbitDetection"アルゴリズムを使う．
  • JuliaSetIterationCountは，次のオプションを取る．
  • MaxIterations 1000使用する反復の最大数
    WorkingPrecision Automatic内部計算精度
  • MaxIterations->n のとき（ただし n は正の整数），z がジュリア集合の外に位置しているかどうかを見るために，関数 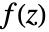は最高で n 回反復される．z がジュリア集合の外側にはない場合，JuliaSetIterationCountは n+1を返す．デフォルト設定はMaxIterations->1000である．
  • WorkingPrecision->n のとき，各反復は内部計算で n 桁精度で計算される．このオプションがない場合，使用する精度は p の精度とMaxIterationsの値に基づいて求められる．

例題

すべて開く すべて閉じる

例  (2)

が のジュリア集合内にないことが分かるまでに，4回の反復が必要である：

Wolfram Language code: JuliaSetIterationCount[z ^ 2 - 1, z, .1 - .2 * I]

数のリストについて，反復回数を計算する：

Wolfram Language code: JuliaSetIterationCount[z ^ 2 - 1, z, {0, 0.5  + 0.5I, 1 + I, 1.5  + 1.5I, 2  + 2I}]

スコープ  (6)

のとき， が のジュリア集合であると分かるまでの反復回数を求める：

Wolfram Language code: JuliaSetIterationCount[-1, .1 - .2 * I]
Wolfram Language code: JuliaSetIterationCount[z ^ 2 - 1, z, .1 - .2 * I]

多項式のジュリア集合に0が含まれるかどうか分かるまでの反復回数を求める：

Wolfram Language code: JuliaSetIterationCount[z ^ 3 - z - 1, z, 0]

有理関数のジュリア集合に0が含まれるかどうかが分かるまでの反復回数を求める：

Wolfram Language code: JuliaSetIterationCount[z ^ 2 / (z ^ 2 - 1), z, 0]

数のリストについて，反復回数を求める：

Wolfram Language code: JuliaSetIterationCount[z ^ 2 / (z ^ 2 - 1), z, {0, 1, 2, 3, 4, 5, 6, 7}]

数の配列についての反復回数を求める：

Wolfram Language code: Shallow[JuliaSetIterationCount[-1, Table[x + I * y, {y, -.01, .01, .0001}, {x, .61, .63, .0001}]]]
Wolfram Language code: MatrixPlot[%]

JuliaSetIterationCountは，あらゆる種類の数に使うことができる：

Wolfram Language code: JuliaSetIterationCount[z ^ 3 - z + 1, z, {-2, -1.979, 1 / 4, 0.26, I, 1 + I, 1 / Pi}]

オプション  (2)

MaxIterations  (1)

必要な反復回数が1000を超える場合は，MaxIterationsを大きくしなければならない：

Wolfram Language code: {JuliaSetIterationCount[0, I + 10 ^ -309], JuliaSetIterationCount[0, I + 10 ^ -309, MaxIterations -> 2000]}

WorkingPrecision  (1)

WorkingPrecisionを大きくすると，確度は上がるがより時間がかかる：

Wolfram Language code: {JuliaSetIterationCount[0, I + 10 ^ -309, MaxIterations -> 2000], JuliaSetIterationCount[0, I + 10 ^ -309, MaxIterations -> 2000, WorkingPrecision -> 1000]}

WorkingPrecisionの設定値を小さくしすぎると，反復が偽ループに入ることがある：

Wolfram Language code: z0 = .618147895647545764; {JuliaSetIterationCount[z ^ 2 - 1, z, z0, WorkingPrecision -> 3], JuliaSetIterationCount[z ^ 2 - 1, z, z0]}

特性と関係  (3)

JuliaSetIterationCount[c]に適用されたArrayPlotは，実質的にJuliaSetPlot[c]である：

Wolfram Language code: JuliaSetPlot[z ^ 2 - 1, z, Method -> "OrbitDetection"]

中央の赤い点はJuliaSetIterationCountが0を返した後のLogを取ったことから来ている：

Wolfram Language code: ArrayPlot[Log@Transpose@JuliaSetIterationCount[z ^ 2 - 1, z, Table[Complex[x, y], {x, -2, 2, .01}, {y, -1, 1, .01}]], PlotRange -> All]

JuliaSetIterationCountはリストに使うことができる．この方が，関数をリストの個々の要素に適用するよりも速い：

Wolfram Language code: First@AbsoluteTiming@ JuliaSetIterationCount[z ^ 2 - 1, z, Table[Complex[x, y], {x, -2, 2, .05}, {y, -2, 2, .05}]]
Wolfram Language code: First@AbsoluteTiming@ Table[JuliaSetIterationCount[z ^ 2 - 1, z, Complex[x, y]], {x, -2, 2, .05}, {y, -2, 2, .05}]

考えられる問題  (1)

点の精度が結果に影響することがある：

Wolfram Language code: {JuliaSetIterationCount[z ^ 2 - 1, z, N[3 / 5, 1]], JuliaSetIterationCount[z ^ 2 - 1, z, N[3 / 5, 100]]}

おもしろい例題  (2)

反復回数を高さとして表示する：

Wolfram Language code: ListPlot3D[Log[1 + JuliaSetIterationCount[z ^ 2 - 1 - I / 3, z, Table[Complex[x, y], {x, -2, 2, .01}, {y, -1, 1, .01}]]]]

パラメータを変えて三次元画像を作成する：

Wolfram Language code: data = Table[JuliaSetIterationCount[(z ^ 2 + c), z, Table[Complex[x, y], {y, -1, 1, .03}, {x, -2, 2, .03}]], {c, -1, 1, 1 / 19}];
Wolfram Language code: Image3D[Rescale[Log[Clip[data, {1, Infinity}]]]]
Wolfram Research (2014), JuliaSetIterationCount, Wolfram言語関数， https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html.

テキスト

Wolfram Research (2014), JuliaSetIterationCount, Wolfram言語関数， https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html.

CMS

Wolfram Language. 2014. "JuliaSetIterationCount." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html.

APA

Wolfram Language. (2014). JuliaSetIterationCount. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html

BibTeX

@misc{reference.wolfram_2026_juliasetiterationcount, author="Wolfram Research", title="{JuliaSetIterationCount}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html}", note=[Accessed: 02-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_juliasetiterationcount, organization={Wolfram Research}, title={JuliaSetIterationCount}, year={2014}, url={https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html}, note=[Accessed: 02-November-2026]}