JuliaSetIterationCount

JuliaSetIterationCount[f,z,p]

返回当以复数 开始进行迭代时，函数 要确定 p 是否属于 f 的朱利亚集合所需要进行的迭代计算次数.

JuliaSetIterationCount[c,p]

返回当以复数 开始进行迭代时，函数 要确定 p 是否属于 的朱利亚集合所需要进行的迭代计算次数.

JuliaSetIterationCount[f,z,{p1,p2,…}]

返回要确定 {p1,p2,…} 是否属于 f 的朱利亚集合所需要进行的相应的迭代计算次数.

JuliaSetIterationCount[c,{p1,p2,…}]

返回要确定 {p1,p2,…} 是否属于 的朱利亚集合所需要进行的相应的迭代计算次数.

更多信息和选项

  • 函数 f 的朱利亚集合是 f 的所有斥性不动点的闭包.
  • JuliaSetIterationCount 和 JuliaSetPlot 一样使用 "OrbitDetection" 算法.
  • 设置 MaxIterations->n，其中 n 是正整数，函数 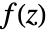将最多被迭代计算 n 次来确定 z 是否不属于朱利亚集合. 如果 z 没有被发现不属于朱利亚集合，JuliaSetIterationCount 返回 n+1. 缺省设置为 MaxIterations->1000.
  • 设置 WorkingPrecision->n 时，运算时将把迭代计算进行到精度 n 位. 如果没有设置该选项，计算精度由 p 的精度或 MaxIterations 的值决定.

范例

打开所有单元关闭所有单元

基本范例  (2)

需要进行四次迭代计算才能确定 不属于 的朱利亚集合：

给定一系列数值，计算相应的迭代次数：

范围  (6)

对于朱利亚集合 ，其中 ，计算 的迭代次数：

对于一个多项式的朱利亚集合，计算0的迭代次数：

对于一个有理函数的朱利亚集合，计算0的迭代次数：

给定一系列数值，计算相应的迭代次数：

给定一个数字数组，计算每个数组元素的迭代次数：

JuliaSetIterationCount 可用于任意数字：

选项  (2)

MaxIterations  (1)

如果需要进行的迭代计算次数超过1000，就必须增大 MaxIterations：

WorkingPrecision  (1)

增大 WorkingPrecision 会提高精度，但需要更多的时间来计算：

如果 WorkingPrecision 太低，将导致迭代进入假循环：

属性和关系  (3)

对 JuliaSetIterationCount[c] 运用 ArrayPlot 等同于 JuliaSetPlot[c]：

中间部位的红点来自于当 JuliaSetIterationCount 返回0以后，取 Log：

对于 JuliaSetIterationCount，将多个数值以列表形式计算比对每个数值单独计算要节省时间：

可能存在的问题  (1)

所给数字的精度可能影响运算结果：

巧妙范例  (2)

用不同的高度来表示迭代次数：

改变参数，生成三维图像：

Wolfram Research (2014)，JuliaSetIterationCount，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html.

文本

Wolfram Research (2014)，JuliaSetIterationCount，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html.

CMS

Wolfram 语言. 2014. "JuliaSetIterationCount." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html.

APA

Wolfram 语言. (2014). JuliaSetIterationCount. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html 年

BibTeX

@misc{reference.wolfram_2024_juliasetiterationcount, author="Wolfram Research", title="{JuliaSetIterationCount}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_juliasetiterationcount, organization={Wolfram Research}, title={JuliaSetIterationCount}, year={2014}, url={https://reference.wolfram.com/language/ref/JuliaSetIterationCount.html}, note=[Accessed: 21-November-2024 ]}