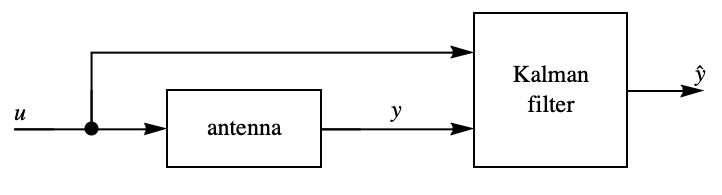
LQEstimatorGains
LQEstimatorGains[ssm,{w,v}]
プロセスノイズと測定ノイズの共分散行列 w と v を伴うStateSpaceModel ssm の最適推定器ゲイン行列を与える.
LQEstimatorGains[ssm,{w,v,h}]
相互共分散行列 h を含む.
LQEstimatorGains[{ssm,sensors},{…}]
ssm のノイズの多い測定として sensors を指定する.
LQEstimatorGains[{ssm,sensors,dinputs},{…}]
ssm の決定論的入力として dinputs を指定する.
詳細とオプション



- 標準状態空間モデル ssm は,連続時間あるいは離散時間においてStateSpaceModel[{a,b,c,d}]として与えることができる.
-
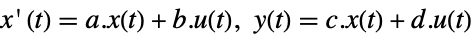
連続時間系 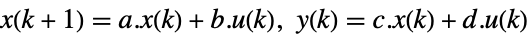
離散時間系 - ディスクリプタ状態空間モデル ssm は,連続時間あるいは離散時間においてStateSpaceModel[{a,b,c,d,e}]として与えることができる.
-
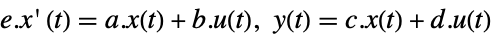
連続時間系 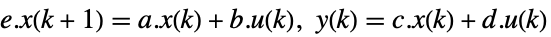
離散時間系 - LQEstimatorGainsは,AffineStateSpaceModelおよびNonlinearStateSpaceModelによって指定される,非線形系もまた許容する.
- 非線形系については,状態変数および入力変数の操作値が考慮され,ゲインは近似テイラー線形化に基づいて計算される.
- 入力
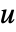 は決定論的入力
は決定論的入力 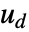 と同様にプロセスノイズ
と同様にプロセスノイズ 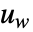 を含むことができる.
を含むことができる. - 引数 dinputs は
 における
における 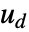 の位置を指定する整数のリストである.
の位置を指定する整数のリストである. - 出力
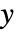 は,他の出力およびノイズの多い測定値
は,他の出力およびノイズの多い測定値  からなる.
からなる. - 引数 sensors は
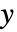 における
における 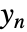 の位置を指定する整数のリストである.
の位置を指定する整数のリストである. - LQEstimatorGains[ssm,{…}]はLQEstimatorGains[{ssm,All,None},{…}]と等価である,
- ノイズの多い測定は
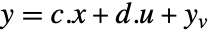 としてモデル化できる.ただし,
としてモデル化できる.ただし,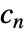 および
および 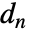 は
は 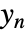 に関連する
に関連する 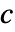 および
および 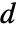 の部分行列であり,
の部分行列であり, はノイズである.
はノイズである. - プロセスノイズと測定ノイズはホワイトノイズおよびガウスノイズであると想定される.
-
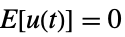 ,
, 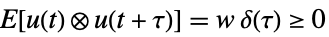
プロセスノイズ 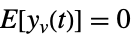 ,
, 
測定ノイズ - プロセスノイズと測定ノイズの間の相互共分散は
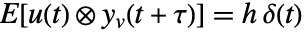 で与えられる.
で与えられる. - 省略された場合,h は零行列であるとみなされる.
- 最適ゲイン
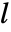 を伴う推定器は
を伴う推定器は 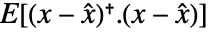 を最小化する.
を最小化する. は推定された状態ベクトルである.
は推定された状態ベクトルである. - LQEstimatorGainsはMethodオプションをサポートする.次の明示的な設定を与えることができる.
-
"CurrentEstimator" 現行推定器の構造 "PredictionEstimator" 予測推定器の構造 - 現行推定値は現在までの測定値に基づいている.
- 予測推定値は直前までの測定値に基づいている.
- 連続時間系の場合,現行の推定器と予測される推定器は等しい.最適ゲインは
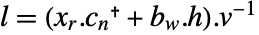 で計算される.
で計算される. は連続代数リッカティ(Riccati)方程式
は連続代数リッカティ(Riccati)方程式 の解である.行列
の解である.行列  はプロセスノイズと関連する
はプロセスノイズと関連する  の部分行列である.
の部分行列である. - 離散時間系の場合,現行推定器の最適ゲイン
 は
は 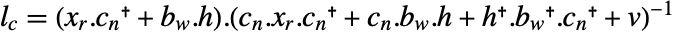 で計算される.
で計算される.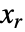 は離散リッカティ方程式
は離散リッカティ方程式 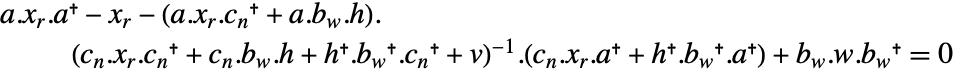 .の解である.
.の解である. - 離散時間系における予測推定器の最適ゲイン
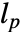 は
は 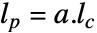 として計算される.
として計算される. - 最適推定器は,
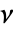 が特異値ではなくペア
が特異値ではなくペア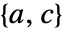 が検出可能で
が検出可能で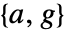 が
が 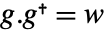 について安定化可能な場合は,漸近的に安定である.
について安定化可能な場合は,漸近的に安定である.
例題
すべて開くすべて閉じるスコープ (7)
特性と関係 (4)
もとになっているリッカティ方程式を使ってKalman推定器ゲインを計算する:
LQEstimatorGainsも同じ結果を返す:
離散時間系のゲインはDiscreteRiccatiSolveで計算できる:
LQEstimatorGainsも同じ結果を返す:
テキスト
Wolfram Research (2010), LQEstimatorGains, Wolfram言語関数, https://reference.wolfram.com/language/ref/LQEstimatorGains.html (2014年に更新).
CMS
Wolfram Language. 2010. "LQEstimatorGains." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/LQEstimatorGains.html.
APA
Wolfram Language. (2010). LQEstimatorGains. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LQEstimatorGains.html