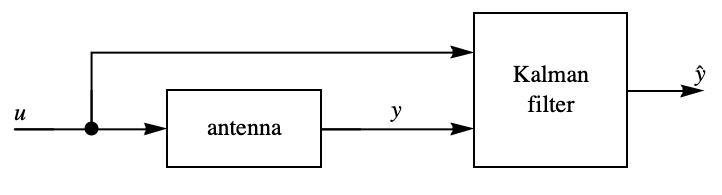
LQEstimatorGains

LQEstimatorGains[ssm,{w,v}]

给出 StateSpaceModel ssm 的最佳估值器增益矩阵，其中过程和测量噪声协方差矩阵为 w 和 v.

LQEstimatorGains[ssm,{w,v,h}]

包括互协方差矩阵 h.

LQEstimatorGains[{ssm,sensors},{…}]

指定 sensors 为 ssm 的噪声测量.

LQEstimatorGains[{ssm,sensors,dinputs},{…}]

指定 dinputs 为 ssm 的确定性输入.

更多信息和选项

  • 在连续时间或者离散时间中，标准状态空间模型 ssm 可以按 StateSpaceModel[{a,b,c,d}] 给出：
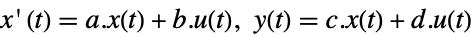
  • 连续时间系统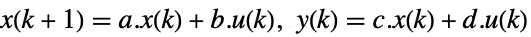
    离散时间系统
  • 在连续时间或者离散时间中，描述器状态空间模型 ssm 可以按 StateSpaceModel[{a,b,c,d,e}] 给出：
  • 连续时间系统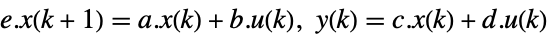
    离散时间系统
  • LQEstimatorGains 也接受由 AffineStateSpaceModel 和 NonlinearStateSpaceModel 指定的非线性系统.
  • 对于非线性系统，考虑状态和输入变量的操作值，并且基于近似泰勒线性化计算增益.
  • 输入 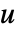可以包含过程噪声 ，以及确定性输入 .
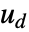  • 参数 dinputs 是指定 在 中的位置的整数列表.
  • 输出 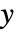包含噪声测量 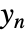以及其他输出.
  • 参数 sensors 是指定 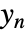在 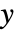中位置的整数列表.
  • LQEstimatorGains[ssm,{…}] 等价于 LQEstimatorGains[{ssm,All,None},{…}].
  • 噪声测量使用 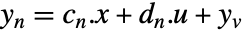建模，其中 和 是与 相关联的 和 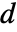的子矩阵，而 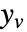是噪声.
  • 过程和测量噪声假设为白噪声和高斯噪声：
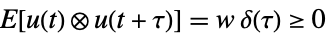
  • , 过程噪声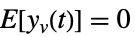
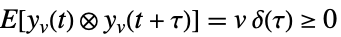
    , 测量噪声
  • 过程噪声和测量噪声之间的互协方差由 给出.
  • 如果省略，假设 h 是一个零矩阵.
  • 用具有优化增益 的估计器最小化 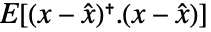，其中 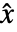是估计的状态向量.
  • LQEstimatorGains 支持 Method 选项. 可给出以下明确设置：
  • "CurrentEstimator"构建当前估值器
    "PredictionEstimator"构建预测估值器
  • 当前估计基于直到当前时刻的测量值.
  • 预测估计基于直到既往时刻的测量值.
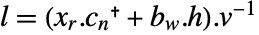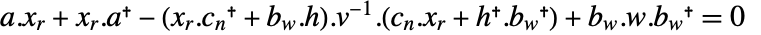  • 对于连续时间系统，当前估值器和预测估值器是一样的. 用 计算最佳增益，其中 是连续代数 Riccati 方程 的解. 矩阵 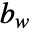是与过程噪声相关的子矩阵 .
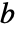  • 对于离散时间系统，用 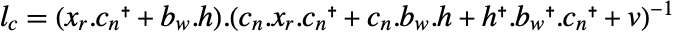计算当前估值器的最佳增益 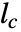，其中 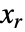是离散 Riccati 方程 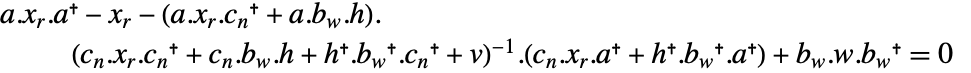的解.
  • 用 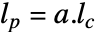计算离散时间系统的预测估值器的最佳增益 .
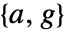  • 最优估值器渐进稳定，如果 是非奇异的，数对 是可检测的，而 对 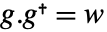是可稳定的.

范例

打开所有单元关闭所有单元

基本范例  (3)

连续时间系统的卡尔曼增益矩阵：

离散时间系统的增益：

不可观测系统的增益：

虽然不可观测，但系统是可检测的：

范围  (7)

确定连续时间系统的优化估计器增益：

具有非零互协方差的离散时间系统的增益：

具有互相关噪声的连续时间系统的卡尔曼增益：

使用第一个输出作为测量：

使用第二个输出作为测量：

最后四个输出是随机干扰的系统的卡尔曼增益：

具有两个确定性输入和两个随机输入系统的估计器增益：

卡尔曼估计器的极点：

求描述器状态空间模型的最优增益：

AffineStateSpaceModel 的增益：

合并估值器：

计算实际和估计响应：

绘制响应的图线：

应用  (1)

计算对随机系统的响应进行平滑的卡曼增益：

具有过程和测量噪声的正弦输入的系统响应：

滤波响应 :

属性和关系  (4)

使用基本的黎卡提（Riccati）方程计算卡尔曼（Kalman）估计器增益：

LQEstimatorGains 给出同样的结果：

使用 DiscreteRiccatiSolve 计算离散时间系统的增益：

LQEstimatorGains 给出同样的结果：

求最优估值器：

它与对偶系统的最优调节器增益的共轭转置等价：

离散时间系统的对偶关系：

可能存在的问题  (2)

测量噪声协方差矩阵必须是正定的：

一个不可观测系统只有它是可检测的情况下，才可以计算优化估计器增益：

最后模式是不稳定的和不可观测的：

Wolfram Research (2010)，LQEstimatorGains，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LQEstimatorGains.html （更新于 2014 年）.

文本

Wolfram Research (2010)，LQEstimatorGains，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LQEstimatorGains.html （更新于 2014 年）.

CMS

Wolfram 语言. 2010. "LQEstimatorGains." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/LQEstimatorGains.html.

APA

Wolfram 语言. (2010). LQEstimatorGains. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LQEstimatorGains.html 年

BibTeX

@misc{reference.wolfram_2024_lqestimatorgains, author="Wolfram Research", title="{LQEstimatorGains}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/LQEstimatorGains.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_lqestimatorgains, organization={Wolfram Research}, title={LQEstimatorGains}, year={2014}, url={https://reference.wolfram.com/language/ref/LQEstimatorGains.html}, note=[Accessed: 21-November-2024 ]}