WOLFRAM

Wolfram 语言与系统参考资料中心

LinearRecurrence[ker,init,n]

给出由线性回归迭代得到的长度为 n 的序列，其中核 ker 的初值为 init.

LinearRecurrence[ker,init,{n}]

给出第 n 项.

LinearRecurrence[ker,init,{nmin,nmax}]

给出第 nmin 项到第 nmax 项.

更多信息
Details and Options Details and Options
范例  
基本范例  
范围  
推广和延伸  
应用  
属性和关系  
可能存在的问题  
巧妙范例  
参见
相关指南
相关链接
历史
按以下格式引用：

LinearRecurrence

LinearRecurrence[ker,init,n]

给出由线性回归迭代得到的长度为 n 的序列，其中核 ker 的初值为 init.

LinearRecurrence[ker,init,{n}]

给出第 n 项.

LinearRecurrence[ker,init,{nmin,nmax}]

给出第 nmin 项到第 nmax 项.

更多信息

  • ker 和 init 可以包含任意符号表达式、数组.
  • 初值列表 init 的长度至少和核列表 ker 相同.
  • 如果 init 的长度大于 ker，仅使用后 Length[ker] 的元素.
  • LinearRecurrence[{a1,…,ad},{y1,…,yd},n] 迭代回归方程 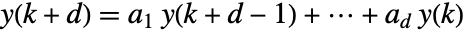，初始条件 、… .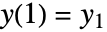
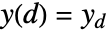  • 系数 ai 和初值 yj 为数组时，则迭代回归被解释为数值和反演系数的点积 .
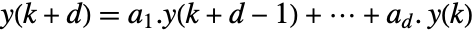  • 如果初值 yj 有维数 {m1,…,ms}，则系数 ai 必须是标量或有维数 {m1,m1}.

范例

打开所有单元 关闭所有单元

基本范例  (3)

Wolfram Language code: LinearRecurrence[{a, b}, {1, 1}, 5]

求解核 {-3, 1} 的一阶微分方程法的一个初值问题：

Wolfram Language code: LinearRecurrence[{-3, 1}, {7, 2}, 10]

求前几个 Fibonacci 数：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1}, 10]
Wolfram Language code: Table[Fibonacci[n], {n, 10}]

范围  (2)

LinearRecurrence 作用于符号核和初值：

Wolfram Language code: LinearRecurrence[{a, b}, {c, d}, 5]

LinearRecurrence 作用于数组：

Wolfram Language code: LinearRecurrence[{1, 1}, {{1, 2}, {2, 1}}, 10]
Wolfram Language code: LinearRecurrence[{{{1, 1}, {0, 1}}, {{1, 0}, {-1, 1}}}, {{1, 2}, {2, 1}}, 6]

推广和延伸  (2)

从给出范围中产生一个子集：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1}, {-5, 5}]

仅给出一个迭代中最后的值：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1}, {5, 5}]

应用  (2)

产生包含 Padovan 序列的递归序列：

Wolfram Language code: LinearRecurrence[{0, 1, 1}, {1, 1, 1}, 10]

Pell 数：

Wolfram Language code: LinearRecurrence[{2, 1}, {0, 1}, 10]

Pell-Lucas 数：

Wolfram Language code: LinearRecurrence[{2, 1}, {2, 2}, 10]

Perrin 序列：

Wolfram Language code: LinearRecurrence[{0, 1, 1}, {3, 0, 2}, 10]

对于较大的 n，以有效方式计算线性回归的第 n 项：

Wolfram Language code: LinearRecurrence[{3, 2, 1, 4}, {1, -36, 9, 80}, {500}]//AbsoluteTiming
Wolfram Language code: LinearRecurrence[{3, 2, 1, 4}, {1, -36, 9, 80}, {500000}];//AbsoluteTiming

属性和关系  (1)

RSolve 求出差分方程的符号解：

Wolfram Language code: RSolve[{a[n + 2] == a[n + 1] + a[n], a[0] == 1, a[1] == 1}, a, n]
Wolfram Language code: Table[a[n] /. %[[1]], {n, 0, 6}]

LinearRecurrence 产生一个程序解：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1}, {7}]

用 RSolveValue 获取同样的结果：

Wolfram Language code: RSolveValue[{a[n + 2] == a[n + 1] + a[n], a[0] == 1, a[1] == 1}, a[6], n]

可能存在的问题  (1)

初值的长度大于核的长度：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1, a, b}, 10]

仅使用最后的项：

Wolfram Language code: LinearRecurrence[{1, 1}, {a, b}, {5, 10}]

巧妙范例  (1)

Wolfram Language code: ListLinePlot[{Re[#], Im[#]}& /@ LinearRecurrence[{Exp[I Pi / Sqrt[2]], I} / 1.1, {1, 1}, 100], PlotRange -> All, AspectRatio -> Automatic]
Wolfram Research (2008)，LinearRecurrence，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LinearRecurrence.html （更新于 2017 年）.

文本

Wolfram Research (2008)，LinearRecurrence，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LinearRecurrence.html （更新于 2017 年）.

CMS

Wolfram 语言. 2008. "LinearRecurrence." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/LinearRecurrence.html.

APA

Wolfram 语言. (2008). LinearRecurrence. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LinearRecurrence.html 年

BibTeX

@misc{reference.wolfram_2026_linearrecurrence, author="Wolfram Research", title="{LinearRecurrence}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/LinearRecurrence.html}", note=[Accessed: 27-October-2026]}

BibLaTeX

@online{reference.wolfram_2026_linearrecurrence, organization={Wolfram Research}, title={LinearRecurrence}, year={2017}, url={https://reference.wolfram.com/language/ref/LinearRecurrence.html}, note=[Accessed: 27-October-2026]}