LinearSolveFunction
LinearSolveFunction[dimensions,data]
行列方程式の解を与える関数を表す.
詳細
- LinearSolveFunction[…]はLinearSolve[m]によって生成される.
- LinearSolveFunctionはFunctionと同じように作用する.
- LinearSolveFunction[…][b]は,特定のベクトルや行列
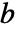 について,行列方程式
について,行列方程式 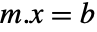 の解を求める.
の解を求める. - dimensions はLinearSolveFunctionが構築されるもとになった行列 m の次元を指定する.
例題
すべて開くすべて閉じるアプリケーション (2)
特性と関係 (2)
Wolfram Research (2003), LinearSolveFunction, Wolfram言語関数, https://reference.wolfram.com/language/ref/LinearSolveFunction.html.
テキスト
Wolfram Research (2003), LinearSolveFunction, Wolfram言語関数, https://reference.wolfram.com/language/ref/LinearSolveFunction.html.
CMS
Wolfram Language. 2003. "LinearSolveFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LinearSolveFunction.html.
APA
Wolfram Language. (2003). LinearSolveFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearSolveFunction.html