Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

LinearSolveFunction

LinearSolveFunction[dimensions,data]

表示一个函数，它给矩阵方程式提供解.

更多信息

LinearSolveFunction[…] 由 LinearSolve[m] 产生.
LinearSolveFunction 的作用与 Function 类似.
LinearSolveFunction[…][b] 对指定的向量或者矩阵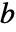，求矩阵方程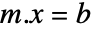的解.
dimensions 指定构建 LinearSolveFunction 的矩阵 m 的维度.

范例

打开所有单元关闭所有单元

基本范例 (1)

一个2×2矩阵：

创建一个函数求解矩阵方程：

当时，求方程中的解：

对于矩阵，求方程中，的解：

范围 (3)

使用精确算法进行计算：

使用机器数算法进行计算：

使用 24 位算法进行计算：

推广和延伸 (1)

得到一个大型稀疏矩阵的因式分解：

显示方程的解：

应用 (2)

求与最小特征值相关的特征向量：

特征值的近似值：

二维拉普拉斯算子有限差近似值的表达式：

逼近拉普拉斯算子的一个矩阵：

矩阵的线性解函数：

单位矩形上泊松方程式的近似解：

单位矩形上泊松方程式的近似解：

属性和关系 (2)

LinearSolveFunction 类似于矩阵求逆. 一个大型的稀疏矩阵：

线性解函数使用的计算时间和内存：

逆矩阵使用的计算时间和内存：

f 与随机向量 b 的逆矩阵相比较：

对一个简单矩阵，创建一个 LinearSolveFunction：

计算 f 的逆矩阵：

使用 Inverse 计算逆矩阵：

可能存在的问题 (1)

无法求出直角矩阵的因数分解：

求出一个解：

顶部