WOLFRAM

Wolfram Language & System Documentation Center

LocalModelFit[data]

creates a smooth approximation of data.

LocalModelFit[data,bw]

approximates data using the bandwidth bw.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Applications  
Sparse Data  
See Also
Related Guides
History
Cite this Page

LocalModelFit

LocalModelFit[data]

creates a smooth approximation of data.

LocalModelFit[data,bw]

approximates data using the bandwidth bw.

Details

  • LocalModelFit, also known as LOESS and adaptive smoothing, creates an approximation of a dataset using local polynomial fitting.
  • Local fitting is typically used for data smoothing in time series analysis, noise reduction in scientific measurements and trend analysis in economic data to reveal underlying patterns without overfitting.
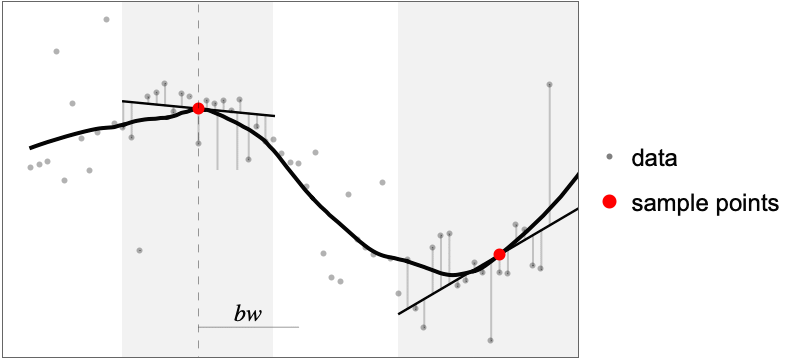
  • For every sample point, the local fitting mechanism involves fitting a low-degree polynomial to a subset of data. Combining the fitted polynomials forms a continuous approximation of the entire dataset.
  • The bandwidth parameter bw determines the scale of locality, where smaller values emphasize local features and larger values smooth out broader trends.
  • For maximum precision, the fit can be computed at every sample point. For faster evaluation, the fit can be precomputed on a fixed number of samples, while the rest is obtained via interpolation.
  • Possible forms of data are:
  • {y1,y2,…}equivalent to the form {{1,y1},{2,y2},…}
    {{x11,x12,…,y1},…}a list of independent values xij and the responses yi
    {{x11,x12,…}y1,…}a list of rules between input values and responses
    {{x11,x12,…},…}{y1,y2,…}a rule between a list of input values and responses
    {{x11,…,y1,…},…}nfit the n^(th) column of a matrix
    Tabular[…]namefit the column name in a tabular object
  • Possible values for bw are:
  • dan absolute size d
    Scaled[f]a fraction f of the points in data
  • The following options can be given:
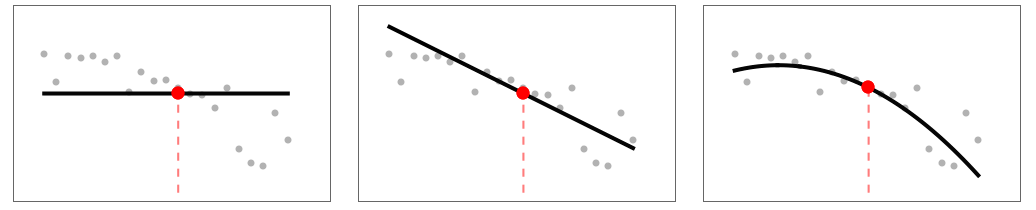
  • ComputeUncertaintyTruewhether to compute confidence bands
    		DistanceFunctionEuclideanDistancethe distance metric to use
    		FitDegree1degree of the polynomial interpolation
    		InterpolationPointsAutomaticwhere the function should be interpolated
  • The value of FitDegree controls the degree of the polynomial interpolation.
  • The value of InterpolationPoints determines the number and placement of the interpolation points.
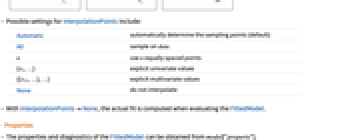
  • Possible settings for InterpolationPoints include:
  • Automaticautomatically determine the sampling points (default)
    Allsample on data
    nuse n equally spaced points
    {x1,…}explicit univariate values
    {{x11,…},…}explicit multivariate values
    		Nonedo not interpolate
  • With InterpolationPointsNone, the actual fit is computed when evaluating the FittedModel.
    • Properties
  • The properties and diagnostics of the FittedModel can be obtained from model["property"].
  • Properties related to the fitted function include:
  • {"BestFit",vars}fitted function at vars
    {"BestFitAround",vars}fitted function with confidence intervals at vars
    {"BestFitDataAround",vars}fitted function with prediction intervals at vars
    "Function"best-fit interpolating function
  • Properties related to data include:
  • "Data"the input data or design matrix and response vector
    "DesignMatrix"design matrix for the model
    "Response"response values in the input data
  • Properties of predicted values include:
  • "FitResiduals"difference between actual and predicted responses
    {"MeanPredictionBands",vars}confidence bands for mean predictions at vars
    "MeanPredictions"confidence intervals for the mean predictions
    "PredictedResponse"fitted values for the data
    {"SinglePredictionBands",vars}confidence bands based on single observations at vars
    "SinglePredictions"confidence intervals for a single predicted response
  • Use model["Properties"] to obtain a list of all the supported properties.

Examples

open all close all

Basic Examples  (1)

Create a smooth interpolation from a dataset:

Scope  (5)

Specify different smoothing bandwidths:

Compute fit uncertainties:

Compute an interpolation at specific points:

Compute a model that can be supports runtime fitting at specific points:

Interpolate 2D points:

Build a smoothed version of the dataset on the sampling grid:

Applications  (1)

Sparse Data  (1)

Test the regression on a a sparse sub-sampling of a dataset:

Build a small, regular sampling grid:

Approximate the data samples on the grid point:

Compare a contour plot of the original data, the sample and the sample approximation:

Wolfram Research (2025), LocalModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/LocalModelFit.html.

Text

Wolfram Research (2025), LocalModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/LocalModelFit.html.

CMS

Wolfram Language. 2025. "LocalModelFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LocalModelFit.html.

APA

Wolfram Language. (2025). LocalModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LocalModelFit.html

BibTeX

@misc{reference.wolfram_2025_localmodelfit, author="Wolfram Research", title="{LocalModelFit}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/LocalModelFit.html}", note=[Accessed: 04-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_localmodelfit, organization={Wolfram Research}, title={LocalModelFit}, year={2025}, url={https://reference.wolfram.com/language/ref/LocalModelFit.html}, note=[Accessed: 04-August-2025]}