WOLFRAM

Wolfram Language & System Documentation Center

KernelModelFit[data]

fits the given dataset data using a default local kernel.

KernelModelFit[data,bw]

uses bandwidth bw for the kernel function.

KernelModelFit[data,bw,f]

uses the specified local kernel f.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Data  
Bandwidth  
Kernel  
See Also
Related Guides
History
Cite this Page

KernelModelFit

KernelModelFit[data]

fits the given dataset data using a default local kernel.

KernelModelFit[data,bw]

uses bandwidth bw for the kernel function.

KernelModelFit[data,bw,f]

uses the specified local kernel f.

Details

  • The KernelModelFit function performs localized data fitting using a specified kernel function.
  • KernelModelFit uses fixed basis expansion, which is commonly used in data analysis fields like signal processing and financial modeling, where capturing local variations is essential.
  • Possible forms of data are:
  • {y1,y2,…}equivalent to the form {{1,y1},{2,y2},…}
    {{x11,x12,…,y1},…}a list of independent values xij and the responses yi
    {{x11,x12,…}y1,…}a list of rules between input values and responses
    {{x11,x12,…},…}{y1,y2,…}a rule between a list of input values and a list of responses
    {{x11,…,y1,…},…}nfit the n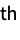^(th) column of a matrix
    Tabular[…]namefit the column name in a tabular object
  • The following bandwidth specifications bw can be given:
  • Automaticautomatically computed bandwidth (default)
    hbandwidth to use
    {bw1,bw2,…}use a bandwidth bwi in dimension i
    {{n1, bw1},…}use ni kernel functions in dimension i
  • With multivariate data such as 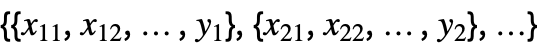{{x_(11),x_(12),... ,y_(1)},{x_(21),x_(22),... ,y_(2)},...}, the number of coordinates xi1, xi2, … should equal the number of input arguments of f.
  • The kernel function f can be an arbitrary expression or one of the following values:
  • Automatic automatically pick the basis function (default)
    "Cauchy"1/(1+x)2fit a Cauchy mixture model
    "Constant"TemplateBox[{{x, /, 4}}, UnitBoxSeq]fit a piecewise constant combination
    "Gaussian"-2 x2fit a Gaussian mixture model
    "Linear"TemplateBox[{{x, /, 2}}, HeavisideLambdaSeq]fit a linear piecewise combination
    fun explicit function
  • If an explicit kernel function f is specified, this function will receive arguments r of the form dist[x,x0]/d, with dist a distance metric, x the prediction point, x0 the central point of the local kernel function and d a scaling factor. Typically, the function f[r] should be positive for 0<=r<=1 to work well. For example, the "Gaussian" mixture model corresponds to f[r]== Exp[-2r2].
  • KernelModelFit has the following options:
  • DistanceFunctionAutomaticdistance metric to use
    IncludeConstantBasisTruewhether to include a constant basis function
    WorkingPrecisionAutomaticthe precision to use
  • ConfidenceLevel95/100confidence level to use for parameters and predictions
    IncludeConstantBasisTruewhether to include a constant basis function
    LinearOffsetFunctionNoneknown offset in the linear predictor
    NominalVariablesNonevariables considered as nominal or categorical
    VarianceEstimatorFunctionAutomaticfunction for estimating the error variance
    WeightsAutomaticweights for data elements
    WorkingPrecisionAutomaticprecision used in internal computations

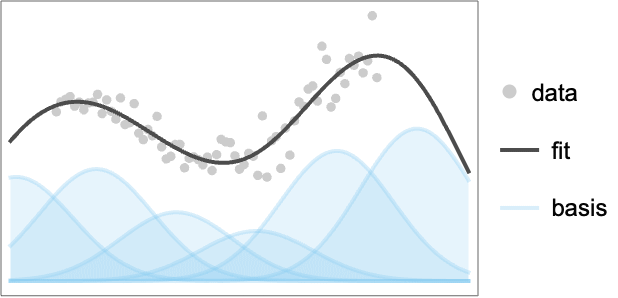
Examples

open all close all

Basic Examples  (2)

Fit a random dataset with a mixture of Gaussians:

Add a piecewise linear approximation to a plot:

Fit a linear kernel model:

Plot the fit together with the original data:

Scope  (8)

Data  (2)

Fit univariate data:

Fit a function with two independent variables:

Bandwidth  (2)

Specify a bandwidth:

Specify a number of kernels and a bandwidth:

Kernel  (4)

Fit a Gaussian kernel:

Fit a Cauchy kernel:

Fit a linear kernel:

Fit a constant kernel:

Wolfram Research (2025), KernelModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/KernelModelFit.html.

Text

Wolfram Research (2025), KernelModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/KernelModelFit.html.

CMS

Wolfram Language. 2025. "KernelModelFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KernelModelFit.html.

APA

Wolfram Language. (2025). KernelModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KernelModelFit.html

BibTeX

@misc{reference.wolfram_2025_kernelmodelfit, author="Wolfram Research", title="{KernelModelFit}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/KernelModelFit.html}", note=[Accessed: 04-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_kernelmodelfit, organization={Wolfram Research}, title={KernelModelFit}, year={2025}, url={https://reference.wolfram.com/language/ref/KernelModelFit.html}, note=[Accessed: 04-August-2025]}