LogIntegral

LogIntegral[z]

is the logarithmic integral function .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
The logarithmic integral function is defined by , where the principal value of the integral is taken.
LogIntegral[z] has a branch cut discontinuity in the complex z plane running from 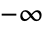to .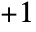
For certain special arguments, LogIntegral automatically evaluates to exact values.
LogIntegral can be evaluated to arbitrary numerical precision.
LogIntegral automatically threads over lists.

Examples

open allclose all

Basic Examples (5)

Evaluate numerically:

Plot over a subset of the reals:

Series expansion at the origin:

Series expansions around the branch point at :

Series expansion at Infinity:

Scope (25)

Numerical Evaluation (4)

Evaluate numerically to high precision:

The precision of the output tracks the precision of the input:

LogIntegral can take complex number inputs:

Evaluate LogIntegral efficiently at high precision:

LogIntegral threads elementwise over lists:

Specific Values (4)

Value at the origin:

Singular point of LogIntegral:

Values at infinity:

Find a zero of :

Visualization (2)

Plot the LogIntegral function:

Plot the real part of :

Plot the imaginary part of :

Function Properties (2)

LogIntegral is defined for all real positive values except 1:

Complex domain:

LogIntegral takes all real values:

Differentiation (2)

First derivative:

Higher derivatives:

Integration (3)

Indefinite integral of LogIntegral:

Definite integral of LogIntegral:

More integrals:

Series Expansions (3)

Taylor expansion for LogIntegral:

Plot the first three approximations for LogIntegral around :

Series expansions on either side of the branch point at :

LogIntegral can be applied to power series:

Function Identities and Simplifications (2)

Primary definition of LogIntegral:

Use FullSimplify to simplify expressions into logarithmic integrals:

Function Representations (3)

Representation through ExpIntegralEi:

Series representation:

TraditionalForm formatting:

Applications (4)

Approximate number of primes less than :

Compare with exact counts:

Plot the real part in the complex plane:

Plot the absolute value in the complex plane:

Find an approximation to Soldner's constant [more info]:

Properties & Relations (4)

Use FullSimplify to simplify expressions into logarithmic integrals:

Use FunctionExpand to write expressions in logarithmic integrals when possible:

Find the numerical root:

Obtain LogIntegral from integrals and sums:

Possible Issues (1)

In traditional form, parentheses are needed around the argument:

Neat Examples (2)

Nested integrals:

Plot the Riemann surface of LogIntegral:

Introduced in 1988

(1.0)

Top