MagneticPDEComponent
MagneticPDEComponent[vars,pars]
磁気PDE項を,変数 vars と pars で与える.
詳細



- MagneticPDEComponentは,静磁気および低周波数の電磁気をモデル変数 vars,モデルパラメータ pars でモデル化するための方程式を生成する.
- MagneticPDEComponentは,偏微分方程式の一部として使う微分演算子の和を返す.
- MagneticPDEComponentは,永久磁石または導電性材料内を流れる低周波数電流によって生成される磁場と電場によって生成される静磁場をモデル化する.
- MagneticPDEComponentは,一般に,電気モーター,コイル,電磁石のモデル化に使われる.
- MagneticPDEComponentは,定常,時間,周波数,パラメータの解析のためのPDEを作成する.
- MagneticPDEComponentは,静磁気および低周波数電磁現象を,独立磁気ベクトルポテンシャル
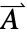 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , "m"}, webers per meter, {{(, "Webers", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , "m"}, webers per meter, {{(, "Webers", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/4.png) ])と独立変数
])と独立変数 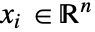 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagneticPDEComponent.ja/6.png) ])でモデル化する.
])でモデル化する. - MagneticPDEComponentは,静磁気の場合は外部電流もモデル化できる.
- 静磁気の場合,電流が存在しない場合はMagnetostaticPDEComponentを使うべきである.
- ベクトル値の従属変数
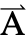 が3-ベクトル
が3-ベクトル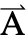 ={Ax1,Ax2,Ax3}として指定される.
={Ax1,Ax2,Ax3}として指定される. - 定常変数 vars は vars={
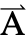 [x1,…,xn],{x1,…,xn}}である.
[x1,…,xn],{x1,…,xn}}である. - 周波数依存変数 vars は vars={
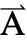 [x1,…,xn],ω,{,…,xn}}である.
[x1,…,xn],ω,{,…,xn}}である. - 時間依存変数 vars は vars={
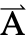 [t,x1,…,xn],t,{x1,…,xn}}である.
[t,x1,…,xn],t,{x1,…,xn}}である. - MagneticPDEComponentは,以下の定常磁気モデルを与える.
- ここで,
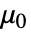 は真空透磁率(単位:[
は真空透磁率(単位:[![TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/14.png) ]),
]),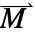 は磁化ベクトル(単位:[
は磁化ベクトル(単位:[![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/16.png) ]),
]),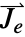 は外部電流密度ベクトル(単位:[
は外部電流密度ベクトル(単位:[![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/18.png) ])である.
])である. - 磁化ベクトル
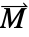 は,磁気特性の強さと方向を示す,材料内の単位体積あたりの磁化双極子モーメントを指定する.s
は,磁気特性の強さと方向を示す,材料内の単位体積あたりの磁化双極子モーメントを指定する.s - MagneticPDEComponentは,以下の周波数領域モデルを与える.
- ただし,真空透磁率
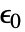 [
[![TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/22.png) ],相対透磁率
],相対透磁率 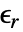 [-],電気伝導率
[-],電気伝導率 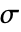 [
[![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/25.png) ],角周波数
],角周波数 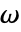 [
[![TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/27.png) ],虚数単位
],虚数単位 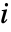 である.
である. - MagneticPDEComponentは,以下の時間領域モデルを与える.
- 磁化ベクトル
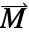 の代替モデルは,残留磁束密度ベクトル
の代替モデルは,残留磁束密度ベクトル 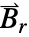 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/32.png) ])である.
])である. - 定常MagneticPDEComponent方程式は以下で与えられる.
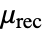 は無単位のリコイル透磁率である.
は無単位のリコイル透磁率である.- 線形材料については,定常方程式MagneticPDEComponentは以下のように簡約される.
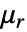 は無単位の相対透磁率である.
は無単位の相対透磁率である.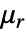 は.等方性,直交異方性あるいは異方性でよい.
は.等方性,直交異方性あるいは異方性でよい.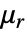 は,磁場の関数でよく,非線形材料を説明することができる.
は,磁場の関数でよく,非線形材料を説明することができる.- 磁気モデル項の単位は[
![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/39.png) ]である.
]である. - 次は,使用可能なパラメータ pars である.
-
パラメータ デフォルト シンボル "ExternalCurrentSource" {0,…} 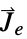 ,外部電流密度ベクトル,単位:[
,外部電流密度ベクトル,単位:[![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/41.png) ]
]"Magnetization" {0,…} 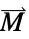 ,磁化ベクトル,単位:[
,磁化ベクトル,単位:[![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/43.png) ]
]"MagneticModelForm" None 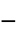
"RegionSymmetry" None 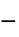
"RelativePermeability" 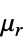 ,無単位の相対透磁率
,無単位の相対透磁率
"RemanentMagneticFluxDensity" {0,…} 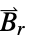 ,残留磁束密度,単位:[
,残留磁束密度,単位:[![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/48.png) ]
]"Thickness" 1 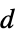 ,厚み,単位:[
,厚み,単位:[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagneticPDEComponent.ja/50.png) ]
] "VacuumPermeability" 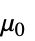
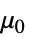 ,真空透磁率,単位:[
,真空透磁率,単位:[![TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/53.png) ]
] - 周波数領域モデルおよび時間領域モデルには,以下の追加的なパラメータが指定できる.
-
パラメータ デフォルト シンボル "ElectricalConductivity" 1 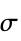 ,電気伝導率,単位:[
,電気伝導率,単位:[![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.ja/55.png) ]
]
- 独立変数の数
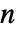 は,
は,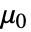 ,
,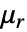 ,
,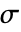 の次元およびベクトル
の次元およびベクトル 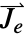 ,
,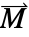 ,
,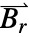 の長さを決定する.
の長さを決定する. - 2D,2D軸対称,3Dの形式のモデルが使用できる.
- 相対透磁率が
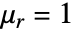 の3D定常モデルについては, "MagneticModelForm"が"FreeSpace"に設定でき,クーロンゲージ条件
の3D定常モデルについては, "MagneticModelForm"が"FreeSpace"に設定でき,クーロンゲージ条件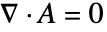 の場合,3D演算子は次のように簡約される.
の場合,3D演算子は次のように簡約される. - 2Dの面外方向の場合,磁気ベクトルポテンシャルには
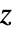 成分しかない.定常線形の場合は,方程式は以下で与えられる.
成分しかない.定常線形の場合は,方程式は以下で与えられる. 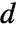 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagneticPDEComponent.ja/69.png) ]は
]は 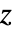 方向の"Thickness"を示す変数で,従属変数
方向の"Thickness"を示す変数で,従属変数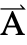 は
は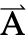 ={0,0,Az}で指定される.
={0,0,Az}で指定される.- パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある.
- "Axisymmetric"領域対称性は,以下のように角変数を削除することで円筒座標が簡約される切断円筒座標系を表す.
-
次元 簡約 例:線形定常方程式 2D 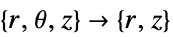
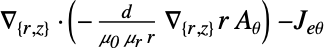
- 方程式を解くためには,共変定式化が利用される.共変定式化は,変数の変更が
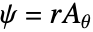 で与えられる軸対称方程式に適用されるメソッドである.
で与えられる軸対称方程式に適用されるメソッドである. - パラメータの入力指定は対応する演算子項についてのそれと厳密に等しい.
- パラメータが指定されていなければ,デフォルトの磁気PDEは以下のようになる.
- MagneticPDEComponentが連想 pars によって…,keypi…,pivi,…]として指定されるパラメータ
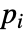 に依存する場合,パラメータ
に依存する場合,パラメータ 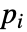 は
は  で置換される.
で置換される.
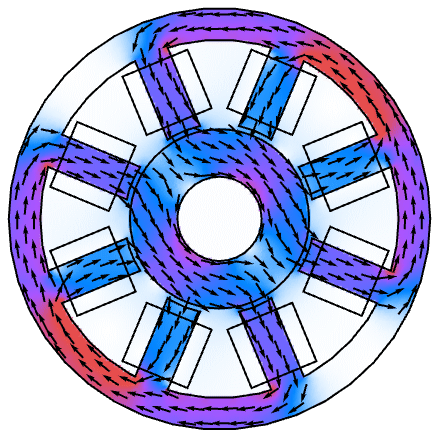
例題
すべて開くすべて閉じるスコープ (7)
面外の記号2D磁気PDEモデルを,真空透磁率 ![]() ,相対透磁率
,相対透磁率 ![]() ,
,![]() 方向への外部電流で定義する:
方向への外部電流で定義する:
デフォルトの磁気PDEモデルを,真空透磁率 ![]() ,相対透磁率
,相対透磁率 ![]() で設定してQuantityオブジェクトを保持する:
で設定してQuantityオブジェクトを保持する:
アプリケーション (2)
Wolfram Research (2025), MagneticPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/MagneticPDEComponent.html.
テキスト
Wolfram Research (2025), MagneticPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/MagneticPDEComponent.html.
CMS
Wolfram Language. 2025. "MagneticPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MagneticPDEComponent.html.
APA
Wolfram Language. (2025). MagneticPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MagneticPDEComponent.html