MagneticPDEComponent[vars,pars]
yields a magnetic PDE term with variables vars and pars.


MagneticPDEComponent
MagneticPDEComponent[vars,pars]
yields a magnetic PDE term with variables vars and pars.
Details






- MagneticPDEComponent generates an equation to model magnetostatics and low-frequency electromagnetics with model variables vars and model parameters pars.
- MagneticPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
- MagneticPDEComponent models static magnetic fields produced by permanent magnets or magnetic and electric fields that are generated by low-frequency electric currents flowing in conductive materials.
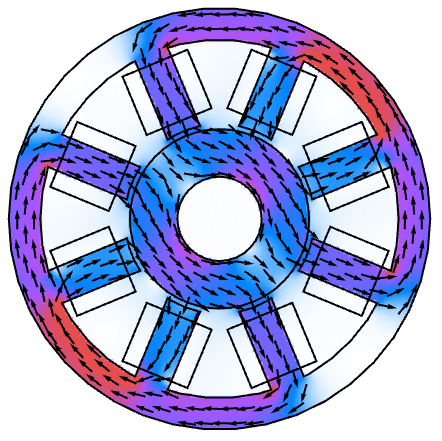
- MagneticPDEComponent is typically used to model electric motors, inductors and electromagnets.
- MagneticPDEComponent creates PDE components for stationary, time, frequency and parametric analysis.
- MagneticPDEComponent models magnetostatics and low-frequency electromagnetic phenomena with the dependent magnetic vector potential
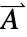 in units of [
in units of [![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , "m"}, webers per meter, {{(, "Webers", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , "m"}, webers per meter, {{(, "Webers", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.en/4.png) ] and independent variables
] and independent variables 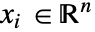 in units of [
in units of [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagneticPDEComponent.en/6.png) ].
]. - MagneticPDEComponent can model external currents also in the static case.
- In the static case, when no currents are present, MagnetostaticPDEComponent should be used.
- The vector-valued dependent variable
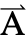 is specified as a three-vector
is specified as a three-vector 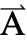 ={Ax1,Ax2,Ax3}.
={Ax1,Ax2,Ax3}. - Stationary variables vars are vars={
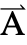 [x1,…,xn],{x1,…,xn}}.
[x1,…,xn],{x1,…,xn}}. - Frequency-dependent variables vars are vars={
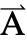 [x1,…,xn],ω,{,…,xn}}.
[x1,…,xn],ω,{,…,xn}}. - Time-dependent variables vars are vars={
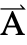 [t,x1,…,xn],t,{x1,…,xn}}.
[t,x1,…,xn],t,{x1,…,xn}}. - MagneticPDEComponent provides a stationary magnetic model:
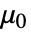 is the vacuum permeability in units of [
is the vacuum permeability in units of [![TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.en/14.png) ],
], 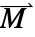 the magnetization vector in units of [
the magnetization vector in units of [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.en/16.png) ] and
] and 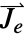 the external current density vector in units of [
the external current density vector in units of [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.en/18.png) ].
].- The magnetization vector
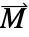 specifies the magnetic dipole moment per unit volume within a material, indicating the strength and direction of its magnetic properties.
specifies the magnetic dipole moment per unit volume within a material, indicating the strength and direction of its magnetic properties. - MagneticPDEComponent provides a frequency domain model:
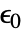 [
[![TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.en/22.png) ] is the vacuum permittivity, relative permittivity
] is the vacuum permittivity, relative permittivity 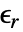 [-], electrical conductivity
[-], electrical conductivity 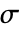 [
[![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.en/25.png) ], angular frequency
], angular frequency 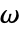 [
[![TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/MagneticPDEComponent.en/27.png) ] and the imaginary unit
] and the imaginary unit 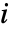 .
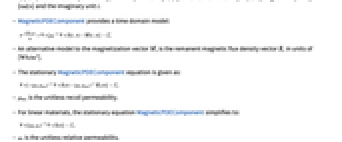
.- MagneticPDEComponent provides a time domain model:
- An alternative model to the magnetization vector
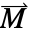 , is the remanent magnetic flux density vector
, is the remanent magnetic flux density vector 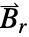 in units of [
in units of [![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.en/32.png) ].
]. - The stationary MagneticPDEComponent equation is given as:
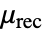 is the unitless recoil permeability.
is the unitless recoil permeability.- For linear materials, the stationary equation MagneticPDEComponent simplifies to:
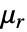 is the unitless relative permeability.
is the unitless relative permeability.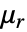 can be isotropic, orthotropic or anisotropic.
can be isotropic, orthotropic or anisotropic.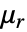 can be a function of the magnetic field and describe nonlinear materials.
can be a function of the magnetic field and describe nonlinear materials.- The units of the magnetic model terms are in [
![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.en/39.png) ].
]. - The following parameters pars can be given:
-
parameter default symbol "ExternalCurrentSource" {0,…} 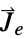 , external current density vector in [
, external current density vector in [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.en/41.png) ]
]"Magnetization" {0,…} 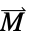 , magnetization vector in [
, magnetization vector in [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.en/43.png) ]
]"MagneticModelForm" None 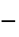
"RegionSymmetry" None 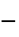
"RelativePermeability" 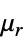 , unitless relative permeability
, unitless relative permeability
"RemanentMagneticFluxDensity" {0,…} 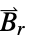 , remanent magnetic flux density in [
, remanent magnetic flux density in [![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.en/48.png) ]
]"Thickness" 1 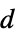 , thickness in [
, thickness in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagneticPDEComponent.en/50.png) ]
] "VacuumPermeability" 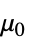
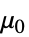 , vacuum permeability in [
, vacuum permeability in [![TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.en/53.png) ]
] - Additional parameters can be specified for the frequency and time domain models:
-
parameter default symbol "ElectricalConductivity" 1 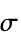 , electrical conductivity in [
, electrical conductivity in [![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.en/55.png) ]
]
- The number of independent variables
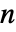 determines the dimensions of
determines the dimensions of 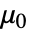 ,
, 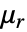 and
and 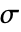 and the length of vectors
and the length of vectors 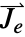 ,
, 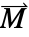 and
and 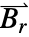 .
. - The models are available in a 2D, a 2D axisymmetric and a 3D form.
- For 3D stationary models with relative permeability
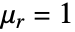 , "MagneticModelForm" can be set to "FreeSpace", and with the Coulomb gauge condition,
, "MagneticModelForm" can be set to "FreeSpace", and with the Coulomb gauge condition, 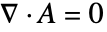 , the 3D operator simplifies to:
, the 3D operator simplifies to: - In 2D, with an out-of-plane direction, the magnetic vector potential has only a
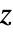 component. In the stationary linear case, the equation is given by:
component. In the stationary linear case, the equation is given by: 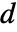 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagneticPDEComponent.en/69.png) ] is a variable denoting a "Thickness" in the
] is a variable denoting a "Thickness" in the 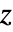 direction and the dependent variable
direction and the dependent variable 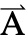 is specified as
is specified as 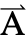 ={0,0,Az}.
={0,0,Az}.- A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
- "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
-
dimension reduction e.g. linear stationary equation 2D 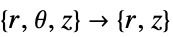
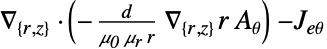
- To solve this equation, the covariant formulation is made use of. The covariant formulation is a method in which a change of variable is applied to axisymmetric equation, given by
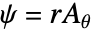 :
: - The input specification for the parameters is exactly the same as for their corresponding operator terms.
- If no parameters are specified, the default magnetic PDE is:
- If the MagneticPDEComponent depends on parameters
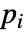 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 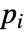 are replaced with
are replaced with 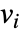 .
.
Examples
open all close allBasic Examples (3)
Scope (7)
Define a magnetic PDE model with a relative permeability set to 5:
Activate a magnetic PDE model:
Define a symbolic 2D out-of-plane magnetic PDE model with vacuum permeability ![]() , relative permeability
, relative permeability ![]() and an external current in the
and an external current in the ![]() direction:
direction:
Note that the ![]() and
and ![]() direction currents are not considered:
direction currents are not considered:
Define a symbolic 2D axisymmetric magnetic PDE model:
Note that the ![]() and
and ![]() direction currents are not considered:
direction currents are not considered:
Define a 3D free-space magnetic PDE model with relative permeability of 1:
Define a symbolic 2D-frequency magnetic PDE model:
Set up the default magnetic PDE model with vacuum permeability ![]() and relative permeability
and relative permeability ![]() and maintain Quantity objects:
and maintain Quantity objects:
Applications (2)
2D Stationary Analysis (1)
2D Frequency Analysis (1)
Define the mesh to model a long copper wire of circular cross section:
Define the parameters of the model with:
Define the uniform external current density in the ![]() direction:
direction:
Define a zero magnetic potential condition at the exterior boundary:
Set up an angular frequency of 800 Hz:
Replace the angular frequency ![]() and solve the PDE:
and solve the PDE:
Tech Notes
Related Guides
History
Text
Wolfram Research (2025), MagneticPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/MagneticPDEComponent.html.
CMS
Wolfram Language. 2025. "MagneticPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MagneticPDEComponent.html.
APA
Wolfram Language. (2025). MagneticPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MagneticPDEComponent.html
BibTeX
@misc{reference.wolfram_2025_magneticpdecomponent, author="Wolfram Research", title="{MagneticPDEComponent}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/MagneticPDEComponent.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_magneticpdecomponent, organization={Wolfram Research}, title={MagneticPDEComponent}, year={2025}, url={https://reference.wolfram.com/language/ref/MagneticPDEComponent.html}, note=[Accessed: 28-February-2026]}