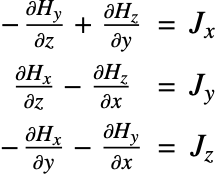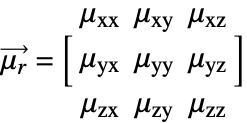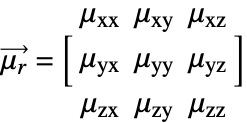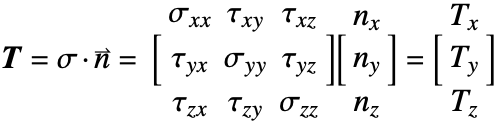Quasistatic Magnetic Fields
| Contents | Boundary Conditions |
| Introduction | Conditions at Material Interfaces |
| Overview Example | Edge/Vector Elements |
| Equations | Nomenclature |
| Secondary Quantities | References |
| Convergence of Magnetic Models |
Contents
Introduction
This monograph uses partial differential equations to model and analyze magnetoelectric fields where the interactions between magnetic and electric fields can be stationary or time or frequency dependent.
The main objective of the PDE presented in this monograph is to consider low-frequency currents and how they induce and interact with a magnetic field. This monograph deals with inductive effects, such as eddy currents. As a special case, low frequency can also mean stationary direct currents, which means a static case. In contrast to the magnetostatic for permanent magnets monograph, this monograph shows how to model static magnetic fields produced not only by permanent magnets but also by stationary direct currents. This monograph does not address wave phenomena, such as diffraction.
The material presented in this monograph is applicable when the skin depth 
is comparable to the device size but the wavelength 
remains much larger than the characteristic size of the device under consideration. This is a complicated way of saying that the equations considered here are applicable when low-frequency currents, compared to the device's size, are present.
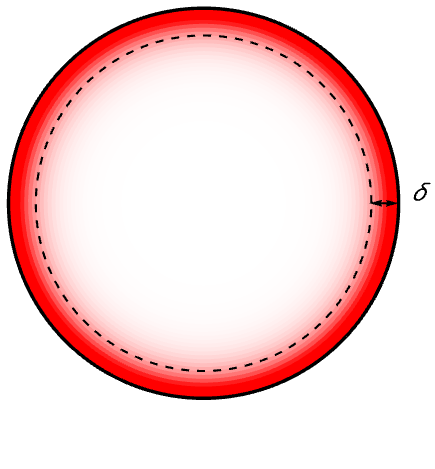
The concept of skin depth 
has been introduced in the Electromagnetics overview monograph and will only be repeated briefly here. The skin effect is illustrated in the figure.
Distribution of current shown in a cross section of a cylindrical conductor. For alternating currents, the current density decreases exponentially from the surface toward the center. The skin depth, 
, is defined as the depth at which the current density is just 1/e of the value at the conductor surface.
When the wavelength 
is much larger than the device size 
, 
, then the device is working in the low-frequency regime. When the skin depth is lower than or equal to the device size, 
, then it is important to consider magnetic and electric fields. Otherwise, it is sufficient to model electric currents according to the Electric Current monograph.
It is necessary to examine these criteria in more detail, to better understand them. First, consider the wavelength criterion. If the wavelength of an electromagnetic wave is much larger than the characteristic size of the object, 
, it means that the time required for the associated electromagnetic wave to propagate at velocity 
over the object size 
is short compared to the simulation time of interest. This means that in a low-frequency regime, with sufficiently slow time variations, the effects of electromagnetic waves are negligible.
The second criterion that needs to be examined is the skin depth. The skin depth 
in [
] is a measure of the depth to which an electromagnetic wave can penetrate an object. The skin effect states that the field intensity depth in a conductor decreases with increasing frequency. For example, the skin depth of copper at 60 [
] is about 8.5 [
]. This means that in a standard 2.5 [
] copper wire, the entire cross section of the wire is utilized for an alternating current flow. At higher frequencies, the skin depth becomes much less, and the alternating current flow becomes more and more confined to the surface of the wire. For example, at 2.4 [
], the skin depth in copper is about 1.33 [
]. This skin effect can be modeled in this monograph.
In the static regime, the electric and magnetic fields are not coupled; this means that when simulating magnetostatic fields, effects such as induced currents do not exist. On the other hand, in the frequency or time-dependent regime, there exists an interaction of electric and magnetic fields, resulting in inductive effects.
In this monograph, magnetic fields are of primary interest and are simulated using the magnetic vector potential formulation. This formulation is derived from Maxwell's equations and from the constitutive relations that relate the interaction of the magnetic and electric fields with matter. In these simulations, the variable to solve for is the magnetic vector potential 
[
]. For this reason, the equation formulation used here is referred to as the 
formulation and is in contract to the 
formulation used in the Magnetostatic monograph.
The magnetic vector potential formulation can be used to model a wide range of devices, from permanent magnets to devices that handle currents, such as inductors and electromagnets. The equation used in the stationary regime is:
where 
is the magnetic vector potential in units of [
], 
is the vacuum permeability in units of [
], 
is the magnetization vector in units of [
], and 
is the external electric current density vector in units of [
].
In the frequency- and time-dependent regimes, an additional term is added to the equation to simulate time-dependent or frequency-dependent fields:
where 
is the electrical conductivity in units of [
], 
is the angular frequency in units of [
], and 
is the imaginary unit.
Modeling electromagnetic devices with partial differential equations (PDEs) is not the only way to model electromagnetic devices. Other techniques include setting up ordinary differential equations (ODEs). This approach is followed by the Wolfram System Modeler. Roughly speaking, the system modeler approach is more suitable for large systems of electromagnetic devices interacting, while the partial differential equation approach is more suitable for a fine-grained analysis of a specific device. In some cases, it is beneficial to use a combination of the two approaches.
The approach taken here is that in the introductory section a simple example is used to introduce a magnetostatic analysis and show the functionality available. This will be followed by more examples to introduce a quasistatic time- and frequency-dependent analysis, then a more theoretical explanation of the underlying ideas and concepts will be given. The theoretical background is much easier to understand once an intuition for the different analyses exists. After that, the available boundary conditions are discussed.
The goal of these analyses is to find the vector potential 
under specific constraints for each case. A subsequent step then finds secondary fields, such as the magnetic flux density 
[
] or the electric current density 
[
]. The analysis and interpretation of these physical quantities are useful to create a better quality engineering design of the device under consideration.
The modeling process as such results in a system of partial differential equations (PDEs) that can be solved with NDSolve.
Extended examples of electromagnetic modeling can be found in the Model Collection.
The electromagnetic device analysis is typically done in stages. First, for the object to be analyzed, a geometric model needs to be created. The geometric model is typically created within a computer-aided design (CAD) process. CAD models can either be imported or created in product. To import geometries, common file formats like DXF, STL or STEP are supported. These geometries can be imported with Import. The alternative is to create the geometrical models in product, for example, by using OpenCascadeLink.
Once the geometric model is made available, some thought needs to be put into what type of analysis is to be performed. The next step is the setup of boundary conditions and constraints. Materials to be used further specify the PDE model. Once the PDE model is fully specified, the subsequent finite element analysis will then compute the desired quantities of the device under investigation. These quantities are then post-processed, either by visualizing them or some derived quantities are computed. This notebook shows the necessary steps for everything except the CAD model generation.
Electromagnetic devices are typically three-dimensional objects. For the models, special cases exist that result in simplified 2D models. In fact, 2D models have been known to solve 90% of the important problems in electrical engineering [Cardoso, 2018].
Many of the animations of the simulation results shown in this notebook are generated with a call to Rasterize. This is to reduce the disk space this notebook requires. The downside is that the visual quality of the animations will not be as crisp as without it. To obtain high-quality graphics, remove or comment out the call to Rasterize.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Overview Example
To illustrate the usage of the finite element method in these subcases of electromagnetics, it is instructive to present a simple example and give an overview of the setup and post-processing steps possible.
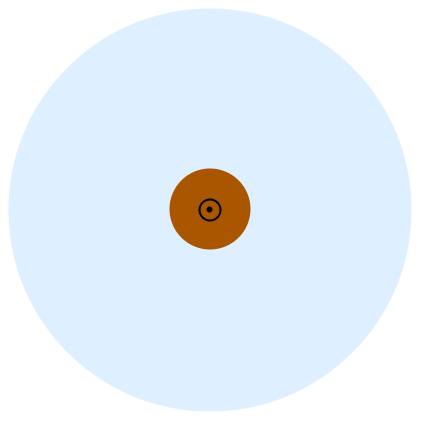
In this first example, the workflow of setting up a magnetostatic PDE model is introduced. To keep things simple, a long wire of circular cross section, carrying a uniform current density in the 
direction, is modeled.
A cross-sectional area of a wire in the
-
plane with a current flowing out of the plane. The notation 
is used to indicate that a vector is coming out of the page.
Creating an electromagnetic model always comprises the same steps:
The dependent variable 
represents the 
component of the vector magnetic potential in the 
and 
directions, respectively. In 2D out-of-plane models, the 
and 
components of the vector magnetic potential are zero.
A relative permeability of one is assumed for the air and copper regions. The copper region will have an external current density of 
.
Note also that in what is essentially a 2D simulation, vector parameters are specified as in 3D, with three components.
The plot shows that the magnetic field circulates counterclockwise around the wire. This is because the current flows out of the plane, in the 
direction.
In this model, DiscontinuousInterpolatingFunction is made use of. The usage and purpose of DiscontinuousInterpolatingFunction is explained in detail in the multiple-materials section.
The next example shows how to perform an axisymmetric magnetic analysis of a Helmholtz coil, using the magnetic vector potential 
formulation.
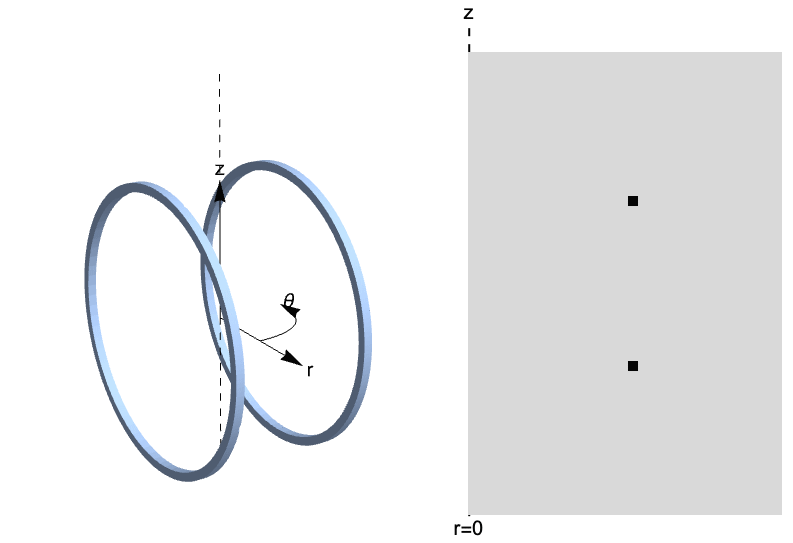
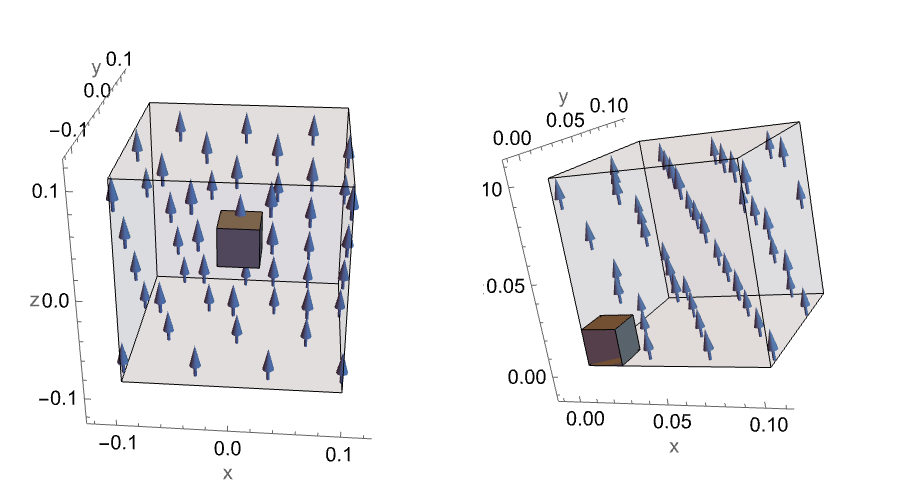
Geometry
Basically, a Helmholtz coil is a device that is made of two identical circular copper coils separated by a distance equal to the coils' radius 
. The coils are aligned in a common axis and carry an equal current in the same direction. The interesting property of this device is that is able to produce an almost uniform magnetic field between the two coils.
The Helmholtz coil geometry is shown below.
On the left: a simulation domain of a 3D Helmholtz coil in a cylindrical coordinate system. To the right: a cross-sectional area of one of the coils in the 
-
plane.
When modeling a magnetic device, it is important to consider the surrounding volume. This approach allows for the simulation of the field that extends outward from the device into the surrounding volume.
The surrounding volume is a type of domain called open or unbounded where its exterior boundaries are known as artificial boundaries. These artificial boundaries limit the extent of the model to a region of interest. A condition must be applied at these outer boundaries to obtain a unique solution.
One needs to be careful and should always define the surrounding region to be sufficiently large compared to the object inside. The reason behind this is to avoid that the boundary conditions applied at the exterior boundaries affect the computations of the field in or on the device.
As the geometry has an axis of revolution, an axisymmetric simulation can be performed. The model reduces to a 2D model with cylindrical independent variables 
-
. More details about axisymmetric models can be found in the Axisymmetric models section.
The 2D version consists in the two cross-sectional areas of the coils with a length 
. Each coil is separated by 
, and the distance between the 
axis and the coils is also of the radius 
. The air area surrounding the device is made up of a rectangle of height 
and length 
.
One thing to keep in mind is the scale used in the geometric model. If the length of the boundary mesh is, for example, in units of meters, then the material parameters will need to be specified in consistent units.
Material Parameters
The next step is to assign material parameters. Generally, all parameters for a electromagnetics model are collected in an Association pars that includes the necessary parameter values.
The default vacuum permeability value 
[
] is used throughout the whole monograph. The "VacuumPermeability" parameter can also be specified if the constant should have a different value, like 1, to scale the equation.
Air and copper are diamagnetic and paramagnetic materials, respectively. These materials respond to magnetic fields in a very different way than ferromagnetic materials, and these effects are very weak. Thus, diamagnetic and paramagnetic materials are regarded as linear and nonmagnetic materials.
So, to express their magnetic properties, a constant relative permeability of 
is used. The relative permeability is used when the materials have a linear behavior; in other words, the magnetic flux density 
is directly proportional to the magnetic field intensity 
. More information about the different types of magnetic materials can be found in the Magnetic materials section.
Material parameters where the values are given as Quantity objects can be used. The exact property names to specify material properties needed can be found on the reference page of MagneticPDEComponent.
Units
Should the units of the geometry be different from the material units, then the material units can be scaled.
Internally, all material data units are converted to "SIBase" units. As a consequence, the default unit of length is "Meters". If the units of the geometry are also in meters, then nothing needs to be changed. If the units of the geometry are not in meters, then either the PDE and material properties need to be scaled to the units of the geometry or the geometry needs to be scaled to "Meters". To scale the units of the PDE and material parameters, the parameter "ScaleUnits" can be given. If not explicitly stated otherwise, examples in this tutorial use the default "SIBase" units.
More information about units used in PDEModels can be found in the PDEModels Best Practice tutorial.
Mesh Generation
To perform a finite element analysis, the boundary mesh representation of the geometric model needs to be discretized into a mesh. In this same process, different material regions are specified with element markers.
The coil regions were refined by using a "MaxCellMeasure" of 
.
Boundary Conditions
Boundary conditions must be defined at physical boundaries to fully specify the problem. In essence, this is done by applying a DirichletCondition or NeumannValue at the boundaries, respectively. Various boundary conditions can be used and will be discussed in the section Boundary Conditions. For the purpose of this overview example, a magnetic vector potential boundary condition will be sufficient.
The purpose of this section is to establish the positions where the boundary conditions are to be applied.
A way to find the positions where the boundary conditions are applied is to visualize them together with the outline geometry defined previously in the geometry section. A magnetic vector potential boundary condition will be applied at all the exterior boundaries and at the axis of symmetry.
For more complicated geometries, the use of markers to specify boundary condition predicates may be more appropriate. For more details about how to define, set up and extract markers from the mesh, one can go to the Markers section of the element mesh generation tutorial.
Magnetostatic Analysis
In a magnetostatic analysis, the primary objective is to determine the magnetic vector potential distribution, 
, and, as secondary derived quantities, the magnetic flux density 
in units of [
] and the magnetic field intensity 
in units of [
].
In a 3D model, the complete vector potential 
is solved for. However, in 2D or 2D axisymmetric models, only the out-of-plane vector potential component is solved for, with the remaining components considered to be zero. This approach assumes that the 
field only exists in the 
-
or 
-
plane and depends solely on the 
and 
or 
and 
spatial variables.
In axisymmetric models, the 
component of the magnetic vector potential 
is the out-of-plane component.
A magnetostatic analysis using the 
formulation in effect solves:
where the dependent variable is the magnetic vector potential 
, which varies with position 
, 
[
] is the vacuum permeability, 
is the unitless relative permeability, and 
is an external generated current density vector. This equation is provided by the function MagneticPDEComponent.
In the 2D axisymmetric case, the above equation simplifies to:
Details on how this equation is derived can be found in the axisymmetric section.
To produce the axisymmetric form of the equation, the parameter "RegionSymmetry" is set to "Axisymmetric".
In this example, both coils are modeled as coils consisting of wound conducting wires, isolated from each other. These coils are excited by applying a current 
to them. This is equivalent to an external current density 
, according to the following relation:
where 
is the number of turns and 
is the cross-sectional area of the coil domain.
Parameters that involve dimensions, such as a vector, are specified as in 3D, with three components.
Note that instead of a single dependent variable, the equation effectively has the product 
. This is in the form of Eqn. 1, shown above. The derivation of the equation is shown in the axisymmetric section. To solve this equation, a change of variable will be performed, for various reasons explained soon.
Two boundary conditions are to be applied here and both are zero magnetic vector potential conditions. One is applied at the exterior boundaries and the other at the axis of symmetry. Applying both boundary conditions has the effect of setting the normal component of 
to zero. More details on this are in the magnetic potential condition section.
In 2D axisymmetric models, a zero magnetic vector potential condition always needs to be specified at the axis of symmetry, 
.
Note that to be consistent with Eqn. 2, the factor 
also appears in the DirichletCondition.
To solve the axisymmetric equation, a change of variable is done. Technically, this means the factor 
is replaced with a new, single dependent variable 
. The change of variable is done for two reasons: first, it offers better numerical stability and accuracy, and second, in the current version of the Wolfram Language, NDSolve cannot do a change of variables automatically. The resulting formulation is called the covariant formulation. The covariant formulation of the magnetostatic equation is explained in detail in the Axisymmetric models section.
A second thing to note is that even though the parameter specification for MagneticPDEComponent was with three component vectors, the function returns a single equation.
The result is an InterpolatingFunction object, which gives the 
distribution.
More information about the solution process and its options can be found in the NDSolve Options for Finite Elements tutorial.
Post-processing
To get the distribution of the 
component of the magnetic vector potential 
, the result needs to be divided by 
, which essentially undoes the change of variables.
Next, the magnetic flux density is computed to see how the field behaves around the coils.
For a three-dimensional model, the function Curl returns a list of three InterpolatingFunction instances with three independent variables 
, 
and 
each. In the 2D axisymmetric case, a list of two InterpolatingFunction instances with the independent variables 
and 
and zero is returned.
Various components of the magnetic field can be accessed by using Part.
In 2D axisymmetric models, the magnetic field only has 
and 
components.
From the vector plot, it can be seen that field rotates clockwise around the coils. The magnitude of the field is almost uniform at left side, the main characteristic of a Helmholtz coil. To better confirm the last statement, the magnitude of the magnetic flux density can be visualized with a DensityPlot.
To visualize the magnetic flux density with DensityPlot, it is necessary to consider the division by 
in the magnetic field expression.
The division by 
produces an infinite expression at 
. So, to compute the magnetic flux density over the entire domain, a special treatment needs to be given to the magnetic field expression at 
.
L'Hôpital's rule, a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives, will be applied to the magnetic field expression at 
.
The plot shows a uniform magnetic flux density in the middle of the region between the coils; the desired field characteristic one wants to achieve with a Helmholtz coil.
Frequency Response Analysis
A frequency response analysis gives information of how a specific variable, in this case, the magnetic vector potential, behaves to a time-varying sinusoidal input such as an alternating current (AC) at a given frequency 
[
]. Through a frequency analysis, one can see inductive effects and compute resistive losses.
In the case of magnetoelectric fields, a frequency response analysis in effect solves the time-harmonic version of the 
formulation equation or its linear form:
where 
is the vacuum permeability, 
is the unitless relative permeability, and 
is the electrical conductivity. This equation can be generated by MagneticPDEComponent and is done by specifying an angular frequency variable 
[
].
The time-harmonic version considers the material's magnetic 
, dielectric 
and conductive 
properties. More details on this can be found in the Time Harmonic section.
The magnetic vector potential 
shown in Eqn. 3 is the complex-valued amplitude of the following function:
where 
is known as a phasor. The solution in a frequency analysis will always be a complex number. More details about phasors can be found in the Time Harmonic section or in the Phasors section of the EM overview monograph.
In the following example, the presence of eddy currents in a cylinder is shown. A conductive cylinder is placed inside a single copper coil, and the coil is excited at a frequency of 100 [
]. The model will be approximated with a 2D axisymmetric version of the 
formulation.
On the left: a simulation domain of a 3D cylinder placed inside a 3D coil in a cylindrical coordinate system. To the right: a cross-sectional area of the coil and cylinder and its surrounding volume in the
-
plane.
In the 2D axisymmetric case, the preceding equation simplifies to:
The conductor has a relative permittivity and permeability of 1, with an electrical conductivity of 
. The coil also will have a permittivity and permeability of 1 and an electrical conductivity of 
.
In a 3D model, the complete vector potential 
is solved for. However, in 2D or 2D axisymmetric models, only the out-of-plane vector potential component is solved for, with the rest considered to be zero. This approach assumes that the 
field only exists in the 
-
or 
-
plane, respectively, and depends solely on the 
and 
or 
and 
spatial variables.
In axisymmetric models, the magnetic vector potential 
is the out-of-plane component.
To produce the axisymmetric form of the equation, the parameter "RegionSymmetry" is set to "Axisymmetric".
In this example, the coil will have a current of 100 000 [
].
A zero magnetic vector potential condition is applied at the exterior boundaries. This has the effect of setting the normal component of 
to zero.
Also, in 2D axisymmetric models, a zero magnetic vector potential condition needs to be specified at the axis of symmetry, 
.
To solve the axisymmetric equation, a change of variable is needed. This means 
is substituted with a new variable 
. This change of variable method is called the covariant formulation. This form of the equation is explained in detail in the Axisymmetric models section.
If multiple frequencies need to be solved for, then using ParametricNDSolve might be helpful, as shown below in the Parametric analysis section.
In this example, the focus is on inductive effects. To visualize the currents, it is necessary to compute the total current density, which in this case is computed from the conduction current and the external current. Before doing that, however, it is necessary to convert the solution to a DiscontinuousInterpolatingFunction and reverse the change of variable to get to the initial variable 
.
In the following lines of code, the different currents are computed.
The plot shows the alternating external current density applied to the coil and how the electromagnetic field generates an induced current inside the conductor and the coil.
A time-varying current induces a time-varying magnetic field, then the magnetic field induces currents in neighboring conductors. These induced currents are called eddy currents.
Parametric Analysis
Sometimes one would like to vary a parameter of a PDE model and repetitively solve the same PDE for a variety of values. A convenient way to do so is a parametric analysis.
As an example, a parametric analysis will be combined with a frequency analysis to study the behavior of the conductor inside the coil and see the different skin depth for the different frequencies.
The purpose of this example is to see the skin effects due to different frequencies.
The electric field is a vector quantity with three components for each direction. In the 2D axisymmetric case, the 
and 
components are zero by definition. Inserting them allows the same workflow to be used as in the 3D case.
The plots show that by increasing the frequency, the skin depth 
gets smaller, causing the currents to flow in the surfaces of the regions. At lower frequencies, the current density flows in all the coils.
Also note how the scale of the plots changes with increasing frequency.
Time-Dependent Analysis
A time-dependent analysis in effect solves the transient 
formulation equation for magnetic fields or its linear form given by:
where 
is the vacuum permeability, 
is the electrical conductivity, and 
is the unitless relative permeability. This equation can be generated by MagneticPDEComponent. This is done by specifying a time variable 
[
]. A detailed derivation is provided in the Transient section.
The transient version of the equation considers magnetic 
and conductive 
properties of a material.
In 2D axisymmetric, the above equation simplifies to:
For the next example, a transient analysis of a conductor inside the coil will be performed. Eddy currents resulting from the coil or source being switched on can then be studied.
To solve the axisymmetric equation, a change of variable is needed. This means to substitute 
with a new variable 
.
This change of variable method is called the covariant formulation. This form of the equation is explained in detail in the Axisymmetric models section.
DiscontinuousInterpolatingFunction does not support time-dependent interpolating functions in the current version.
The animation shows that initially the magnetic field slightly penetrates the conductor and the coil. After the current reaches a steady state, the skin depth increases and the magnetic field then extends deeper into the conductor.
Equations
In this monograph, the magnetic vector potential formulation, also called the 
formulation, is used for modeling magnetic fields. This section will derive the magnetic vector potential formulation for the static and quasistatic cases. Quasistatic refers to a situation where the time variations of the electromagnetic fields are slow enough that the system can be approximated as being in a near-static state. The equation will be derived from Maxwell's equations.
The 
formulation is used in contrast to the 
formulation. The 
formulation is used to model current-free magnetostatics and is explained in the magnetostatic monograph. In this monograph, with the 
formulation, currents are considered. Considering a current density vector, 
, makes a new formulation necessary, the 
formulation.
The most general form of the equation of the quasistatic time-dependent 
formulation is given by:
The source term 
in units of [
] denotes an external current density vector within the domain and is explained in detail in the current density vector section. The dependent variable in this equation is the vector magnetic potential 
in units of [
]. 
can vary with position 
and time 
. There is a time-derivative term 
with time 
[
] and with 
the electrical conductivity in units of [
]. The equation is made up of a curl-curl term 
with the vacuum permeability 
[
] as the coefficient, a curl term 
in which the variable 
[
] is the magnetization vector. 
and 
can also vary with position 
and time 
.
The 
formulation equation will be derived next. As a start, Maxwell's equations are given. In general, Maxwell's equations can be written in the following form:
where 
is the gradient operator, 
is the dot product and 
is the cross product. All vector-valued quantities are bold. 
[
] and 
[
] are the electric and magnetic field intensities, respectively. 
[
] is the electric flux density, and 
[
]
[
] is the magnetic flux density, sometimes also called magnetic induction. A flux density refers to a flow though an area. 
[
] is the electric current flux density, commonly called electric current density, and 
[
] is electric charge density, and they represent sources of magnetic and electric fields, respectively. SI units are used throughout the monograph.
Maxwell–Ampere's law
Maxwell–Ampere's law describes the behavior of both electric and magnetic fields. It relates the magnetic field 
around a closed loop to the electric current, 
, passing though the loop, and also accounts for changes in an electric field 
:
At low frequencies, currents and electromagnetic fields vary slowly, the displacement currents 
are small compared with the conducting currents 
and the displacement currents can be neglected. This simplifying assumption is at the core of the equations presented in this tutorial. With this assumption, known as the quasistatic approximation, Maxwell–Ampere's law can be rewritten as:
The equation 
can be expressed in component form. In three-dimensional space with the magnetic field intensity components 
and electric current 
, the component form of the equation is given by:
Magnetic and electric potentials
In electromagnetism, many equations are written in terms of the fields 
and 
or equivalently, in terms of the potentials 
and 
.
The magnetic vector potential 
is a vector field, and the electric potential 
[
] is a scalar with the relations:
By choosing a clever mathematical transformation, known as gauge fixing and explained later, the electric field 
can be rewritten in terms of 
only:
All analysis types shown in this monograph involve only 
.
Constitutive equations—Material models
The constitutive equations describe how the material properties of a medium influence the magnetic field. For the 
formulation, two constitutive equations are considered, one for the 
field and one for the 
field.
The first constitutive equation relates the magnetic field intensity 
with the magnetic flux density 
and the magnetization 
within a material:
where 
is the vacuum permeability. If there is a linear relation between 
and 
, then the constitutive equation can be simplified to
where 
is the relative permeability. This is explained in more detail in the Linear magnetic materials section.
The second constitutive equation relates the current density vector with the electric field 
and an external current density vector 
:
The part 
is known as Ohm's law. In Ohm's law, the relation between the electric field and the current density vector is linear, where the proportionality constant is the electrical conductivity 
.
Quasistatic 
formulation equation
The quasistatic equation is then constructed by rewriting the quasistatic version of Ampere's law
in terms of the constitutive laws , 
and 
leading to
and then expressing the equation in terms of 
though 
and 
:
This gives a rough outline of the derivation of the quasistatic 
formulation equation. The next sections drill a bit deeper into the derivation.
Maxwell–Ampere's Law
The original law of Ampere states that a magnetic field relates to an electric current 
. Maxwell's addition states that magnetic field additionally relates to a changing electric field. Maxwell called this changing electric field displacement current. In this monograph, the differential form of Maxwell–Ampere's equation is used:
Quasistatic approximation
In order to avoid solving the full Maxwell equations, simplifications and assumptions are made. At the core of the 
formulation is the quasistatic approximation. Additional information about the quasistatic approximation can be found in the Low-frequency regime-quasistatic section of the electromagnetics overview page.
A quasistatic analysis implies that the time required for an electromagnetic wave to propagate at velocity 
over the object size 
is short compared to the time of interest 
:
where the ratio 
is the time required for an electromagnetic wave to propagate through a length 
. Put into different words, Eqn. 4 can be reformulated in terms of the wavelength 
by 
. Equivalently, the wavelength can be expressed as 
, where 
is a frequency. If the wavelength 
is much larger than the object size 
, then electromagnetic radiation is negligible:
Neglecting electromagnetic radiation means the changes in the electric or magnetic field are treated as instantaneous and are not considered.
Also, the induced displacement currents are ignored, 
, and Maxwell–Ampere's law simplifies to the original Ampere's law:
Magnetic and Electric Potentials
The main idea is to not solve the full set of Maxwell equations, as this is resource intensive. To do so, the electromagnetic equations are reformulated in terms of the magnetic and electric potentials. This will lead to a single equation involving only one dependent variable, the dependent magnetic vector potential 
.
The relation between the magnetic vector potential 
and the magnetic flux density 
is hidden in Gauss's law for magnetism:
Generally speaking, for fields, the following equation can be deduced:
which states that the divergence of the curl of any vector field is zero. To satisfy 
, the magnetic flux density can be represented as:
where 
is the curl of a vector field, called the magnetic vector potential 
.
The electric potential 
[
] is derived from the time-independent Faraday's law, 
, which states that 
is curl free. Generally speaking, for fields, the following equation can be deduced:
which states that the curl of the gradient of any scalar function 
is zero. Comparing Eqn. 5 with Faraday's law, it can be deduced that 
can be represented as the gradient of a function 
:
The negative sign was placed by convenience and for historical reasons.
Now, to derive the electric field 
in terms of the magnetic vector potential 
, two steps are taken. In the first, an expression involving both 
and 
is found, and in the second step that will be further reduced to only depend on 
.
First, it is necessary to modify the definition of 
so it is consistent with Faraday's law:
To satisfy Faraday's law, the following expression is proposed:
To check that this is correct, the expression is substituted into Faraday's law:
Since the curl of a gradient is zero 
, the equation becomes:
and since 
, the equation again becomes Faraday’s law:
This confirms that the expression
As a summary, 
can be expressed in terms of 
and 
can be expressed in terms of 
and 
.
Now, it is important to realize that the magnetic and electric fields are not uniquely defined through the potentials. This is because both 
and 
are only present in the equations through derivatives. But a unique solution is needed. To solve this issue, gauge transformations are introduced. A gauge transformation is a mathematical transformation of the potentials 
or 
without altering the physical observables, such as the electric and magnetic fields. Just like one can add a constant to 
and the gradient remains the same, one can add a gradient to 
and the curl remains the same. This concept will be explained in more detail in the subsequent sections. It is this gauge transformation that will then also eliminate the potential 
.
On the uniqueness of the solutions
Consider the case of the magnetic vector potential 
. A different magnetic vector potential 
could be equally defined as:
where one adds the gradient of a scalar function, for instance 
, to 
. The use of 
will lead to the same magnetic flux density 
, since the general identity 
holds:
In the case of the electric potential, a potential 
can be equally defined as:
The use of 
will lead to the same electric field 
, since the terms 
and 
cancel out:
The function 
is called the gauge function, and choosing a particular 
is called gauge fixing. In general terms, these variable transformations of the potentials are called gauge transformations. Now, in order to have a unique solution for potentials, a specific gauge has to be applied to the potentials.
Two gauge transformations are used in this monograph, and they will be explained in the following sections.
Gauge transformation for 
In dynamic cases, the electric field is dependent on 
and 
through 
. What is desired, however, is to have a single equation to describe both magnetic and electric fields. This would imply solving for just a single dependent variable. It is possible to do a gauge fixing through 
such that the scalar electric potential 
vanishes and only the magnetic vector potential 
remains. The time harmonic and transient equations provided by MagneticPDEComponent produce equations with this specific gauge fixing.
To derive this gauge 
, 
needs to equal 0. For that, 
is forced to be zero:
Balancing the equation and integrating both sides, the following definition for 
is obtained:
where 
is an arbitrary function of spatial coordinates and is the integration constant. By selecting this specific 
, it is ensured that the transformed scalar potential 
is zero:
The term 
vanishes as it is time independent.
In this new gauge where 
, the electric field 
simplifies to:
Since the gauge transformation did not change the electric field 
, the field can be rewritten as:
This means that in this specific gauge fixing, the electric field is entirely determined by the time variation of the magnetic vector potential.
Using Eqn. 6 will allow the electric field 
associated to the electric current density 
to be described in terms of the magnetic vector potential:
This approach allows an equation to be formulated that describes both magnetic and electric fields using a single variable: the magnetic vector potential 
This approach is valid for the low-frequency, the quasistatic case.
What remains to be done is to also fix 
, since that is also not uniquely defined and a unique solution to the equation (7) cannot be found.
Coulomb's gauge for A
Helmholtz's theorem, the fundamental theorem of vector calculus, states two things: First, a vector field 
can be decomposed into a curl-free part and a divergence-free part. It also states that if both 
and 
are given and boundary conditions are applied, then 
is uniquely defined.
It is important to mention that 
is always unique, even if 
is not. This can be seen when one inserts
This will give the same 
since 
.
So far, only the curl of 
is specified. A common choice is to then add a constraint to fix the divergence of 
:
This is called Coulomb's gauge fixing. Together with boundary conditions, the equations are then fully specified.
In 2D and 2D axisymmetric models, the Coulomb's gauge fixing is automatically satisfied.
Constitutive Equations
The constitutive equations in electromagnetics are mathematical relationships that describe how electric and magnetic fields interact with materials. They are fundamental to understanding and solving Maxwell's equations in different media. In this monograph, the constitutive equations relate the electric field 
and the current density 
, the magnetic field intensity 
and the magnetic flux density 
, with the properties of a material.
The magnetic constitutive equation describes how the magnetic flux density 
is related to the magnetic field intensity 
in a material and is given by:
where 
[
] is the magnetization vector and is a vector field that expresses the density of permanent or induced magnetic dipole moments in a material.
More details on the magnetic constitutive equation can be found in the Magnetostatics for Permanent magnets monograph in the magnetics materials section.
Next, the constitutive law that relates the electric field 
and the current density 
is explained in detail.
Ohm's law
In a conductor, the current density vector 
in units of [
] is always associated with an electric field 
[
], and this relation is expressed in Ohm's law as follows:
where 
is the electrical conductivity in units of [
].
A more general version of Ohm’s law includes an externally generated current density
and is given by:
where 
does not have an electric field 
associated with it.
Since in the context of magnetostatics there are no currents associated with the electric field in a conductor, the term 
vanishes. The only contributions to 
will be given by an external current density 
:
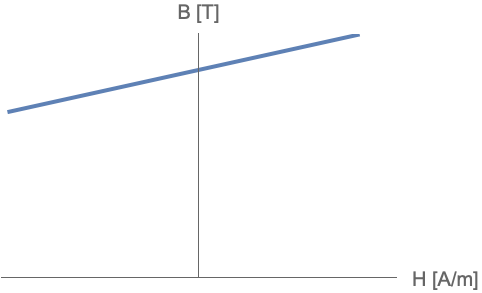
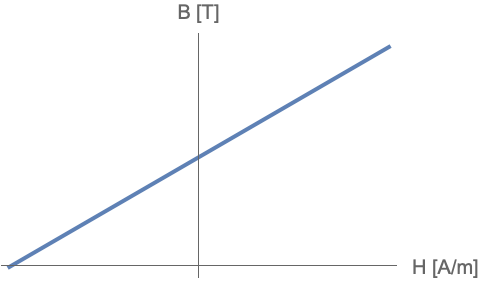
Linear magnetic materials
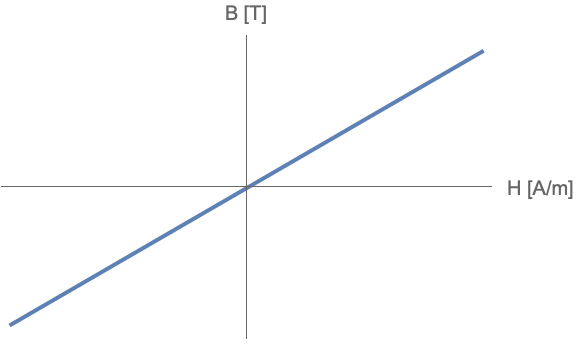
In certain magnetic materials, the magnetic flux density 
will have a linear relationship with the magnetic field intensity 
. This behavior is seen in linear magnetic materials.
For linear materials, 
depends linearly on 
such that:
where 
is a dimensionless quantity called magnetic susceptibility that measures how susceptible a material is to a magnetic field.
Substituting Eqn. 8 into 
yields the linear constitutive relation for magnetic materials:
where the unitless 
is the relative permeability given by:
and 
is the absolute permeability in units of [
].
The relative permeability can depend on the space coordinates 
and vary in the region considered, i.e. an inhomogeneous material, or vary with direction, i.e. an anisotropic material.
Anisotropic materials
For anisotropic materials, like crystals, the relative permeability 
is a tensor. In the 3D case, the tensor has nine components:
where 
is the relative permeability tensor. 
and 
are called the principal relative permeability coefficients and off-diagonal permeability coefficients, respectively.
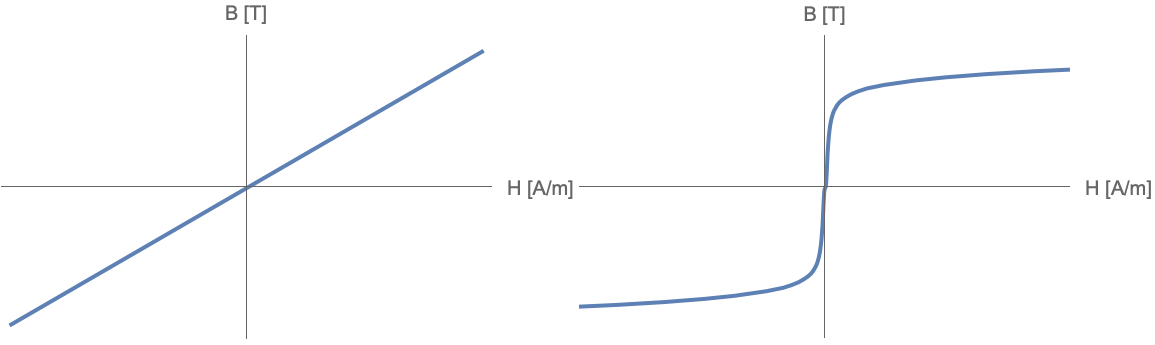
Classification of Magnetic Materials
In general, the relative permeability 
or the magnetic susceptibility 
is used to classify materials depending on their response to external magnetic fields. There are basically two types of magnetic materials:
- Hard ferromagnetic materials, better known as permanent magnets. Permanent magnets are made from alloys, such as mixtures of neodymium, iron and boron (NdFeB), or from an alloy primarily composed of aluminum, nickel and cobalt (AlNiCo).
A material is said to be nonmagnetic if 
or 
, such as free space or air.
A detailed description of soft and hard magnetic materials is provided in the Magnetostatics for Permanent Magnets monograph in the Classification of magnetic materials section.
Quasistatic 
formulation Equation
Now that the Maxwell–Ampere's law, the potentials and the constitutive equations have been discussed in detail, a proper derivation of the quasistatic time-dependent equation can be shown.
The 
formulation is derived from Ampere's law:
First, the constitutive relation between 
and 
, 
, is substituted into Eqn. 9:
Then, by substituting the current density vector (Eqn. 10):
Finally, the equation is rewritten in terms of the magnetic vector potential 
using 
and 
:
In the time-dependent case, magnetic fields are produced by time-dependent currents associated with an electric field.
In the time-dependent analysis, electric fields are considered and because of that, inductive and skin effects are considered.
If one wants to verify if a model requires an analysis that considers inductive effects, a rule of thumb is to check if the skin depth 
of the object considered is equal to or lower than the characteristic size 
of the object: 
. If the skin depth is much larger than 
and magnetic fields are of no interest, then one can perform a simple electric current simulation, explained in the electric current monograph.
The 
formulation equations shown all along the monograph can be generated by MagneticPDEComponent. To make use of this PDE operator, variables vars and parameters pars need to be set up.
Quasistatic time-dependent equation setup
The time-dependent equation is given by:
To specify a PDE model, model variables vars need to be set up. In the 
formulation, the main variable is a vector 
; in 3D, the variables are the three components of the vector 
, but in 2D and 2D axis, different components can be solved for. There are three different ways to specify the components, which are the following:
Why there are different options for 2D and 2D axisymmetric models? The choice of components of the magnetic vector potential is equivalent to the direction of the current density vector. By selecting a specific direction for the magnetic vector potential, the direction of the applied currents in the model is controlled: out-of-plane currents, in-plane currents or currents flowing in all three coordinates. The most common option is to solve for the out-of-plane component in 2D and 2D axisymmetric models, resulting in out-of-plane currents and in-plane magnetic fields, which is the default option.
An in-plane or three-component vector potential in 2D and 2D axisymmetric cases is not implemented in the current version of the Wolfram Language.
Time-dependent variables for 3D models are specified as 
, where 
is the time variable in units of [
].
Time-dependent variables for 2D models are specified as 
.
Time-dependent variables for 2D axisymmetric models are specified as 
.
For more details of 3D models, 2D models and 2D axisymmetric models, check their respective sections.
in the 
direction, a magnetization vector 
and an electrical conductivity 
:For time-dependent cases, the following magnetic parameters pars can be used:
The use of "Magnetization", "RelativePermeability" and "RemanentMagneticFluxDensity" is shown in the Modeling magnetic materials section.
Quasistatic Harmonic 
formulation
The quasistatic time-harmonic equation is derived from the quasistatic time-dependent equation:
expresses time and space dependence.
In the time-harmonic case, it is assumed that the fields are time-harmonic fields. A field is referred to as time harmonic if it can be expressed as a sine function with a specific frequency. These fields are expressed in complex-valued form using phasors.
By convention, the phasor is often expressed simply as:
When the phasor equation is inserted in the transient equation, the equation simplifies to a time-independent equation. The phasor equation expresses the time-dependent potential as a product of the potential amplitude 
with the time factor 
.
The remaining fields and vectors can also be expressed through phasors. For example, the electric field has an amplitude function 
and the same time factor 
.
The transient equation in terms of phasors is:
The curl term 
can be rewritten as:
since the 
term does not depend on space. This leads to:
Next, the first-order time-derivative terms are considered and expanded:
Reinserting the expanded terms into Eqn. 11 gives:
Factoring out the common terms 
and 
, the equation simplifies to the time-harmonic equation:
In the frequency case, magnetic fields are produced by alternating currents (AC).
This PDE is a time-independent equation. Because it is a time-independent PDE, it can be solved more efficiently compared to the time-dependent equation.
For a linear materials, a sinusoidal input will yield a sinusoidal output. This property is fundamental for a time-harmonic analysis. In contrast, for nonlinear materials, this linearity property does not hold, and therefore, harmonic analysis cannot be applied to nonlinear materials. In the case of nonlinear materials, a full time-dependent simulation is necessary.
Frequency-dependent equation setup
The frequency-dependent equation is given by:
Frequency-dependent variables for 3D models are specified as 
, where 
is the angular frequency. Note that in this case- the angular frequency 
is not an argument of the dependent variable.
Frequency-dependent variables for 2D are specified as 
.
Frequency-dependent variables for 2D axisymmetric models are specified as 
.
For more details of 3D models, 2D models and 2D axisymmetric models, check their respective sections.
in the 
direction, a magnetization vector 
, an electrical conductivity 
and a relative permittivity 
:For frequency cases, the following magnetic parameters pars can be used:
The use of "Magnetization", "RelativePermeability" and "RemanentMagneticFluxDensity" is shown in the Modeling magnetic materials section.
Steady-State 
formulation
In the static regime, time variations of quantities become zero, 
. A direct consequence of neglecting the time-derivative terms in Maxwell's equations is that the electric and magnetic fields are no longer coupled.
As Maxwell's equations are no longer coupled, it is possible to solve solely for the electric or magnetic field.
The static equation used in the 
formulation is derived from Ampere's law 
or by just neglecting the time-derivative term, 
, of the quasistatic time-dependent equation:
In the steady-state case, magnetic fields are produced either by direct currents (DC) or, alternatively, by permanent magnets.
The main difference between the MagnetostaticPDEComponent and the static version of the MagneticPDEComponent is that the latter allows for an external current 
.
Magnetostatic equation setup
The most general magnetostatic equation in the 
formulation is given by:
Stationary variables for 3D models are specified as 
, where the dependent variables are the components in all three directions of the magnetic vector potential in units of [
] and the {x,y,z} are the independent, spatial variables in units of [
].
Stationary variables for 2D models are specified as 
.
Stationary variables for 2D axisymmetric models are specified as 
.
For more details of 3D models, 2D models and 2D axisymmetric models, check their respective sections.
The following is a list of possible parameters pars that can be specified for an 
steady magnetostatic model:
The use of "Magnetization", "RelativePermeability" and "RemanentMagneticFluxDensity" is shown in the Modeling magnetic materials section.
2D Out-of-Plane Models
When there is only an axial excitation and/or the magnetic field varies only in the 
and 
directions, a 3D model can be simplified to a 2D model in the 
-
plane.
In the two-dimensional case with an out-of-plane direction, an axial excitation 
that is independent of 
is assumed, and thus, the magnetic vector potential has only a 
component that satisfies the following equation:
where 
[
] is a thickness variable denoting thickness in the 
direction.
Expanding the curl operators, 
, this equation becomes:
where the curl-curl nature of the equation turns into a simple diffusion equation 
that can be represented with a DiffusionPDETerm.
The default value for the thickness is 
.
Parameters that involve dimensions, such as a vector, are specified as in 3D, with three components.
Note that this model definition uses inactive PDE operators. "Numerical Solution of Partial Differential Equations" has several sections that explain the use of inactive operators.
As 
and 
are zero, the only vector fields components of 
and 
that matter are the 
and 
components, which are parallel to the 
-
plane. After solving for 
, the magnetic flux density can be computed from 
.
Other constitutive relations in 2D, such as magnetization 
, only need have the 
and 
components of 
. The third component of the "Magnetization", 
, is ignored.
In the case of a 2D out-of-plane model, a unique solution for 
is obtained because Coulomb's gauge is always satisfied automatically. To verify this, the Coulomb's gauge condition is given by:
2D out-of-plane models example
As a 2D application example, a permanent magnet and its surroundings are modeled. A 3D cuboid is cut at 
and is modeled as a rectangular cross section. The magnet is magnetized transversely in the direction of the 
axis. A zero magnetic vector potential is used at the exterior boundaries of the surrounding volume to enclose the field.
Since in the default case the element size in the red magnet region is roughly the same as the magnet itself, the magnet region was refined to get a better accuracy in the solution.
The magnet will have a magnetization in the 
direction with a value of 
. The air region will have a magnetization of zero.
2D Out-of-Plane Axisymmetric Models
An axisymmetric simulation can be performed when a 3D solid has an axis of revolution. An axisymmetric model uses a truncated cylindrical coordinate system in 2D with independent variables 
instead of the cylindrical coordinates 
. The cylindrical coordinate variable 
disappears because the system is rotationally symmetric about the 
axis.
In the two-dimensional axisymmetric case, the electric current is assumed to have only a 
component 
that is independent of 
. The magnetic vector potential has only a 
component that satisfies the following equation:
The 2D magnetostatic axisymmetric equation for 
for linear materials is given as:
An axisymmetric model has the advantage that the computational cost in both time and memory is much less than in the case of solving a full 3D model.
To solve this equation, the covariant formulation is made use of. The covariant formulation is a method in which a change of variable is applied to Eqn. 12, given by 
:
The covariant formulation offers a better numerical stability and accuracy when solving 2D axisymmetric models.
The MagneticPDEComponent function can produce the axisymmetric form of the 
magnetostatic equation. To do so, the parameter "RegionSymmetry" is set to "Axisymmetric".
A 2D axisymmetric model can also be generated when using other constitutive relations such as 
.
Parameters that involve dimensions, such as a vector, are specified as in 3D, with three components.
In the case of a 2D out-of-plane axisymmetric model, a unique solution for 
is obtained because Coulomb's gauge is satisfied automatically. To verify this, the Coulomb's gauge condition is given by:
3D Models
In 3D models, it is necessary to solve for all components of the magnetic vector potential 
. So, in contrast to the 2D and 2D axisymmetric versions, the equation remains as a curl-curl equation.
One needs to take special care when modeling 3D models with the magnetic vector potential. The first challenge comes from the fact that the current version of Mathematica does not support vector elements. Vector elements are also known as edge elements. When solving for more than a single vector component, the standard nodal elements that Mathematica provides are not the best choice. The fact that vector elements are currently not implemented, however, does not mean that one cannot use nodal elements to model 3D magnetostatic models with the magnetic vector potential.
So, even though it is possible to use nodal elements to solve the full 3D models, a direct consequence is that nodal elements force the normal component of 
at a surface to be continuous everywhere. This means that interface conditions that express discontinuities at the interface between different media cannot be fulfilled completely.
Additionally, imposing boundary conditions on curve boundaries is complicated using nodal elements.
For these reasons, it is recommended to use the magnetic scalar potential 
to model 3D magnetostatic models if they are free of currents. An additional benefit of the magnetic scalar potential 
formulation is that it is less computationally expensive and needs less memory to solve. In the case that the model is not current free and a 2D simplification cannot be justified, then and only then a full 3D model should be considered.
When creating a 3D model, one needs to remember that in order to obtain a unique solution for 
, a gauge condition needs to be imposed.
If the 3D magnetostatic model has a relative permeability of 1, then an alternative equation to the curl-curl equation can be used, which is better suited for nodal elements and is explained in the Special case: Magnetostatics in free space section.
3D model example
In the next example, a 3D magnet cylinder will be modeled using the 
formulation. The magnet will be surrounded by a cuboid. The choice of the cuboid is to specify easier 3D boundary conditions.
The cylinder will have a magnetization of 1x10^5 in the z direction.
A magnetic insulation boundary will be applied at the exterior boundaries. This means that the tangential components of the magnetic vector potential at the boundaries will be set to zero.
Special case: Magnetostatics in free space
In 3D models, the curl-curl equation can be simplified if the material model is linear and has a relative permeability of 1. This is interesting because free space has a relative permeability of one and is a useful simplification. For the linear material model and with 
, the 
formulation becomes:
together with the Coulomb gauge condition (
), the following equation is obtained:
This Poisson-type equation is used for 3D models and it works well with nodal elements. To generate the equation, the parameter "MagneticModelForm" is set to "FreeSpace".
In the next example, the Poisson type equation is used to model a single bar of copper that carries a current in the 
direction. The geometry is composed of the copper bar and an air domain that surrounds the bar. The exterior domain has the form of a rectangle.
To specify the different region, region markers are used.
The current will flow in the 
-direction with a value of 
.
The boundary conditions at the walls are a set of magnetic insulation conditions for each component of 
that is parallel to the bar. To specify the boundaries, point element markers are used. The markers that belong to the parallel walls are: 1, 2, 3 and 4. To know which point element marker to use, one needs to know the boundary element markers that belong to each surface.
Then, with SelectPointMarkerFromBoundaryMarker, one can select from which surfaces the point markers should be constructed. Details on this process are found in the Markers section of the Element Mesh generation tutorial.
Next, a visualization of the magnitude of the magnetic vector potential and of the magnetic flux density will be shown.
Next, the 
field is computed. This is done by converting the vector potential 
into a discontinuous interpolating function. The DiscontinuousInterpolatingFunction is explained in detail in the multiple-materials section.
Modeling Magnetic Materials
This section mostly follows the section of the same name in the Magnetostatics for Permanent Magnets monograph, however, it supplements it with static magnetic examples using the 
formulation.
There are many different ways to represent the behavior of a magnetic material. The choice of which model or constitutive relation to use depends on how much of the material's characteristics are intended to be incorporated.
There are basically two types of magnetic materials that can be modeled:
- Hard ferromagnetic materials, better known as permanent magnets. Permanent magnets are made from alloys, such as mixtures of neodymium, iron and boron (NdFeB), or from an alloy primarily composed of aluminum, nickel and cobalt (AlNiCo).
The next sections explain in detail how to model soft and hard magnetic materials and make use of them in MagneticPDEComponent through its different parameters inputs.
The use of a full 
-
curve with hysteresis is not really needed in many cases. The following sections show how to model magnetic material if hysteresis is not to be considered. This will be appropriate in many, if not most cases. This will significantly simplify the models.
Soft magnetic materials
For soft magnetic materials like diamagnetic or paramagnetic materials, one can often simply use a relative permeability 
to describe the material.
A linear relationship between 
and 
, given by 
.
For soft ferromagnetic materials, one can often simply use a relative permeability 
to describe the material or use a nonlinear 
, which can often be obtained from a simplified 
-
curve.
The constant relative permeability is used in soft irons if the fields are small, and a nonlinear 
is typically used to include the effect of magnetic saturation in soft ferromagnetic materials. To do so, the nonlinear 
is often fitted with a fitting function.
The figures below illustrate the types of simplified 
-
curves that are used to model soft ferromagnetic materials. Since a soft ferromagnetic material does not exhibit a big hysteresis, the 
-
curves used can be simpler than the ones presented in the Ferromagnetic materials section.
On the left: A linear relationship between 
and 
, given by 
. On the right: A nonlinear relationship between 
and 
, given by 
.
In the next section, a motor model that uses a nonlinear relative permeability 
obtained from a 
-
curve is shown.
In this example, the static magnetic flux density of an electric motor is to be found. This example looks at a simplified model of a motor.
In the following representation of the motor geometry, the stator sections are gray, the rotor is red, and the blue area represents air. Also, several coils are grouped and displayed in orange, light orange and yellow. So, different magnetic materials will be modeled at the same time. For the air and coils, a relative permeability of one 
. For the stator sections and rotor, a nonlinear relative permeability will be used.
Cross section of a simplified electric motor. The stator sections are in gray, the rotor in red, the coils in orange, light orange and yellow, and the blue area represents air.
The 
out-of-plane 2D model is going to be used in this example since the currents only flow orthogonal to the 
and 
planes, generating magnetic fields only in the 
-
plane. In this example, it is assumed that the permeability is constant in the 
direction.
In order to identify each subregion, element markers are used. For markers to be attributed to different subregions, coordinates lying in those subregions need to be specified.
Visualizing the boundary mesh and the marker coordinates helps one to understand the process of specifying marker coordinates. For the visualization, it is necessary to group the marker coordinates and set up colors that will go with the markers.
The coils, currently visualized with an orange point, are to carry different currents. To simplify this process, each coil will get a marker assigned such that coils carrying the same current are grouped together.
A list of coordinates lying in the subregions has been created, with markers attributed to those coordinates.
In the next lines of code, a nonlinear relative permeability will be defined through a given 
-
curve.
Two options exist: one is to create an interpolating function from the data, and the second is to generate a fit. The second option is more efficient, so in the end, the second option will be used to run the simulation.
From the plot, it is evident that this data belongs to the first quadrant of a typical 
-
curve.
The permeability will be given by the relation of 
and 
.
While generating the interpolation, make sure that the smallest and largest values of the 
-
curve are continued if the interpolating function is queried outside of its domain. Also instruct the interpolating function to not give warning messages when queried outside of the domain.
With the interpolating function approach comes great flexibility. However, a more efficiently evaluatable approach is to find a fit for the 
-
curve data.
The nonlinear permeability will depend on the norm of the magnetic flux density, so it must be defined first.
If the relative permeability coefficient is evaluated either in the rotor or the stator, then the ferromagnetic material will be used. In all other regions, the 
for air is used.
The current density in the coils is specified such that there is a positive current in elements with ElementMarker 4, a negative current in the elements with ElementMarker 6 and a zero current elsewhere.
The boundary condition is set up in such a way that the magnetic potential is zero at the out rim of the stator.
As a final step, the norm of the magnetic flux density and the vector field will be visualized. This model utilizes the DiscontinuousInterpolatingFunction, as explained in the multiple-materials section.
Hard ferromagnetic materials: Permanent magnets
In the following section, constitutive relations for permanent magnets are described, including:
The following sections show how to model hard ferromagnetic material if hysteresis is not to be considered. This will be appropriate in many, if not most, cases.
The rare case where a full 
-
curve with hysteresis needs to be considered can be handled through the Jiles–Artherton model but is not considered here. Details on this model can be found in [Kumar & Tummuru, 2016].
A conceptually simple approach to modeling permanent magnets is to describe the magnet though a magnetization vector 
according with the following equation:
This constitutive relation is used to describe rare earth permanent magnets that are already magnetized and that remain in this state.
In the figure below, the 
-
behavior is illustrated by 
, where 
is the offset of the line and the slope is 
.
The 2D out-of-plane example shows how to set up a model with a magnetization.
An alternative constitutive relation used to model permanent magnets is the remanent magnetic flux density. In general, manufacturers of permanent magnets provide magnetic characteristics in the form of a demagnetization curve, which is the second quadrant of the 
-
plane. These curves indicates the remanent flux density 
and the coercive field intensity 
and generally describe the way in which 
and 
vary in the second quadrant. Permanent magnets, such as neodymium-iron-boron (NdFeB), exhibit an almost linear demagnetisation curve as shown in the following picture:
Simple 
-
behavior given by 
used for hard ferromagnetic materials.
This constitutive law follows:
where 
is the remanent flux density in units of [
] and 
is the unitless recoil permeability. Compared to the magnetization approach, this relation improves the modeled quality by the effect of demagnetizing caused by an externally applied field in the opposite direction to 
.
The recoil permeability 
is given by the ratio 
/
. The value of 
given by manufacturers is actually the remanent flux density norm. To get the 
vector, the given value of 
is multiplied with a normalized direction field 
.
Using Eqn. 13 turns the magnetic vector potential equation into:
In time-dependent models, it is possible to consider the entire hysteresis loop of a magnetic material. For this, the Jiles–Atherton model is used, which is not considered here.
Modeling Anisotropic Materials
For anisotropic materials, like crystals, the relative permeability 
is a three-by-three tensor. In the 3D case, the tensor has nine components:
where 
is the relative permeability tensor. 
and 
are called the principal relative permeability coefficients and off-diagonal permeability coefficients, respectively.
An anisotropic relative permeability can be use in both of the formulations.
Anisotropic materials are found in advanced composite materials, magnetic recording media and certain types of sensors. These materials are used in fields like geophysics, material science and electrical engineering [Gutfleisch et al., 2011].
Modeling Multiple Materials
In magnetostatic models, the simulation domain always consists of multiple materials, primarily because it is necessary to account for the surrounding volume of a magnetic device.To show the process for simulating multimaterial domains, an electromagnet will be modeled.
Consider a solenoid with a finite-length iron core. In this example, the magnetic flux density will be determined for a geometry consisting of a coil and an iron core embedded inside a cylindrical air domain. As the electromagnetic system has a symmetry around the 
axis, an axisymmetric 2D model will be used.
On the left: A simulation domain of a 3D electromagnet in a cylindrical coordinate system. To the right: a cross-sectional area of the electromagnet in the 
-
plane, where the core is in gray and the coil in orange.
The use of element markers will be employed here to give the different material properties to the subdomains.
A current density of 
will be flowing through the coil.
The iron core will have a relative permeability of 1000 while air and coil have a relative permeability of 1.
The use of Piecewise allows an efficient evaluation of the PDE coefficients; it is discussed in detail in the section Efficient Evaluation of PDE Coefficients of the Finite Element Method Usage Tips tutorial.
A zero magnetic vector potential is applied at the axis of symmetry, at 
, and at all exterior boundaries.
To solve the axisymmetric equation, a change of variable is done. Technically this means the factor 
is replaced with a new, single dependent variable 
.
To get the distribution of the 
component of the magnetic vector potential 
, the result needs to be divided by 
, which essentially undoes the change of variables.
Also note that the plot shows that the magnetic vector potential is continuous across the iron/air and copper/air interfaces. Now, let's proceed to study the material interfaces and their impact on the secondary fields. When computing the magnetic flux density 
or the magnetic field intensity 
, it is crucial to consider that at interfaces between materials, the fields can exhibit discontinuities. More information about these conditions can be found in the section on Conditions at material interfaces. Exploring how to handle these discontinuous interfaces is essential.
In this example, 
will exhibit a discontinuity at the iron/air interface at 
and between 
and 
.
The above plot shows the discontinuity across the material interface running along 
. The values observed are 
from the left and 
from the right simultaneously.
Note that when using InterpolatingFunction, there is no control over what the value of the field at the interface is, which can be seen by the jiggled plot line. When evaluating an InterpolatingFunction at the material interface, it is somewhat random if the value of the one material subregion or the other subregion is given.
To address this issue, DiscontinuousInterpolatingFunction or EvaluateOnElementMesh is employed. This process will be shown next.
First, 
is converted to a DiscontinuousInterpolatingFunction and then 
.
The magnetic flux density 
will then be computed in a second step.
The plot no longer shows random values from one of material subregions. The plot shows only values that belong to the air subregion.
The remaining discontinuities observed in the plot are of a different nature. These arise when taking the derivative of the primary unknown variable, 
in this case. Such secondary values can exhibit discontinuities at the element boundaries. While these discontinuities are unavoidable, they can be reduced by refining the mesh. For more details, refer to the Discontinuity of Secondary Unknown Quantities section in the PDE Models Best Practices tutorial.
Note that the value that is returned at the discontinuity is the value of air. The behavior of what takes precedence over what can be controlled. DiscontinuousInterpolatingFunction or EvaluateOnElementMesh functions will prioritize a value from one of the subregions. The default is based on the order of material markers.
In this case, the default prioritization favors the air region over the rest of the regions. To demonstrate the usage of marker prioritization, fields will be recalculated with a priority that favors the iron core region over the air region.
With this technique, precise control is exerted over which material subregion takes precedence. DiscontinuousInterpolatingFunction is very useful to compute values at the interface between two distinct materials, which can then be used in plots or as arguments for further computations.
Secondary Quantities
Once the simulation is completed, the solution for the dependent variables is obtained. Especially for the 
formulation, there is an interest in quantities derived from the primary dependent variable, as the magnetic vector potential 
does not have a physical meaning. These derived quantities are called secondary quantities. Secondary quantities provide a deeper understanding of the model and include quantities like fields, forces, energy and energy-related parameters.
Fields
There are two different fields that can be computed from the magnetic vector potential 
, the magnetic field intensity 
and the magnetic flux density 
.
The magnetic flux density is computed with the following equation:
The equation to use for computing the magnetic field intensity 
will depend on the constitutive relations used, in the case of a linear material, 
is computed with the following equation:
Energy
The magnetostatic energy 
is the energy that is stored in a magnetic field. For linear materials, the magnetostatic energy can be expressed by the following equation:
where the magnetostatic energy density 
is:
For nonlinear materials that have a hysteresis effect, the previous equation no longer applies and a more general expression is needed to account for the hysteresis effect.
For nonlinear materials, the energy density is obtained by integrating the 
relationship:
where 
is the integration variable. The integration limit is from 0 to 
, indicating a start from an unmagnetized state up to the current state 
. Integration over the entire volume yields the total energy:
In the next example, the total magnetic energy is computed of a magnetic field produced by a simple coil.
On the left: A simulation domain of a 3D coil in a cylindrical coordinate system. To the right: a cross-sectional area of the coil and its surrounding volume in the
-
plane.
As the geometry has an axis of revolution, an axisymmetric simulation can be performed. The model reduces to a 2D model with cylindrical independent variables 
-
. More details about axisymmetric model are found in the Axisymmetric models section.
The 2D geometry consists of a cross-sectional area of the coil with radius 
. The distance between the 
axis and the coil is 
. The air area surrounding the device is modeled with a half-disk of radius 
.
The model is made of an air and a coil region, so to assign different material parameters, region markers are used. Both materials have a relative permeability of 
.
A max cell measure value is applied to the mesh to get a more accurate result.
A current of 
[
] will be flowing through the coil.
At the axis of symmetry, at 
, a zero magnetic vector potential boundary condition is applied to implement the symmetry boundary condition.
In this model, the goal is to compute the energy stored in the magnetic field. To proceed, the magnetic fields must first be computed.
The magnetostatic energy is given by:
Note that in the integrand, a factor of 
is added because this is an axisymmetric case. Specifically, the 
term arises when performing a volume integral in cylindrical coordinates, and the 
factor accounts for the theta contribution of the volume integral.
Inductance
Inductance is a property of a conductor to oppose a change in the electric current flowing through it. This opposition of current comes from the induced voltage caused by the magnetic field that is produced by the current flowing through the conductor, according to Faraday's law of induction. Devices that have this property are often called inductors. The inductance, 
, is measured in units of Henry [
] and is defined as the ratio of the induced voltage to the rate of change of the current. The inductance can also be equal to the ratio of the magnetic flux 
[
] to the current 
[
] flowing through a device:
The inductance given by Eqn. 14 is also referred to as self-inductance. The inductance 
is a parameter of how much magnetic energy can be stored in an inductor. Thus, the inductance 
can also be computed from a known magnetic energy of the inductor. The magnetic energy stored in an inductor is expressed as:
From Eqn. 15, the inductance can now be expressed in terms of 
:
To show how an inductance can be obtained, the inductance 
of the coil model, which was used in the energy section, will be computed
The accuracy of the inductance value can be improved if a mesh refinement study or a convergence test is performed with the model.
Magnetostatic Forces
This section shows how to compute magnetostatic forces between objects. Computing forces can be necessary for several reasons in various engineering and scientific applications. For example, many devices rely on magnetostatic forces for control and actuation.
Two methods are shown here. The first method is only applicable as long as the objects have a current flowing through them and is based on the Lorentz force equation. The second method is more general and can be used to compute forces between permanent magnets or between different magnetic materials. This second method uses the Maxwell stress tensor 
.
Lorentz force
In electromagnetism, the Lorentz force is the force that a point charge experiences due to an electromagnetic field. A particle of charge 
moving with a velocity 
in an electric field 
and a magnetic field 
experiences a force 
[
] of:
To keep things simple, in the case of magnetostatics only, electric fields are not considered and the Lorentz force takes the following form:
For a continuous charge density distribution 
in motion, the equation is:
where 
is in units of [
], 
[
] is the volume charge density and 
[
] is the current density vector.
The total force is the volume integral over the charge density distribution:
So, in the magnetostatic case, wherever information about the current density vector and the magnetic field 
is available, values for the forces between various objects can be obtained.
Maxwell stress tensor
The Maxwell stress tensor 
is used to calculate electric and magnetic forces on objects. With the Maxwell stress tensor, the force can generally be expressed as:
where 
is the Maxwell stress tensor, 
is the unit normal vector, 
is the differential surface, 
is the domain surface boundary, 
is the domain volume, 
is the differential volume, and 
is the Poynting vector.
The componentwise definition of the Maxwell stress tensor is:
where 
is the magnitude of E and 
is the Kronecker delta, which is 1 if the indices are the same and zero otherwise.
Again, to keep things simple, in the magnetostatic case, there are no time dependencies and the equation simplifies to:
The componentwise Maxwell stress tensor simplifies to:
The first index 
indicates the direction of the force and the second index 
indicates the direction of the surface.
In a 3D case, with spatial variables 
, the Maxwell stress tensor has nine components, as follows:
The Maxwell stress tensor 
is a force per unit area acting on a surface. To compute the actual stress 
for a given surface, one takes the dot product with the desired surface normal such that:
Then, 
is integrated over the surface of the object that the force acts on:
For the complete derivation of the equation, refer to [Griffiths, 2017]. Eqn. 16 can be reformulated [Ida & Bastos, 2013] and give the equivalent formula:
Eqn. 17 is an alternative to compute 
and is used here.
Example: Force between a current-carrying wire and a magnetic cylinder
In the next example, both methods will be used to compute the magnetostatic force between a current-carrying wire and a magnetic cylinder parallel to the wire. Assuming these two objects are infinitely long, the problem can be treated as a 2D model.
Region markers are used in this example.
As the goal of this section is to compute forces on boundaries, an especially accurate mesh is constructed. To obtain a refinement at the internal boundaries of the domain, boundary mesh is manually generated. Furthermore, if a NumericalRegion is used. The use of a NumericalRegion provides advantages when integrating the force expressions as it allows NIntegrate to be used with a better accuracy.
To manually generate the boundary mesh, the idea is to generate each part of the region separately and then combine them in a new boundary mesh.
More details on this matter can be seen in the Element Mesh generation tutorial in the Numerical Regions section.
The magnet will have a relative permeability of 
and air of 1.
The wire will be the only object to have a current flowing through.
A magnetic insulation boundary condition is set at the exterior boundaries.
When forces are computed at an interface between different magnetic materials, one should pay special attention to the computed fields. At the interface, the magnetic field intensity 
and the magnetic flux density field 
can show discontinuities.
To address a discontinuity, DiscontinuousInterpolatingFunction or EvaluateOnElementMesh can be used. These functions will prioritize the value from one of the subregions. The default priority is based on the marker order given in "MeshElementMarkerUnion". To change the priority, the "MarkerPriority" option can specified. This procedure is explained in more detail in the multiple-materials section.
In this case, the default priority prioritizes the air region over the magnetic region, which is sensible here.
First, the 
component of the force on the wire is computed using Eqn. 18:
At the interface between the wire and air, there are no discontinuities because the relative permeability is the same.
The integral of Eqn. 19 is performed only in the wire region, so a new element mesh is needed.
Now that the force on the wire has been computed, the force on the magnetic cylinder can be computed next. For that, the Maxwell stress tensor will be used:
The force on the wire and its reaction force on the magnetic cylinder have approximately the same magnitude, in spite of using completely different equations for the force.
Convergence of Magnetic Models
Typically when an electromagnetic simulation is to be performed, the device of interested is surrounded by a second domain representing the material in which the device is embedded. This surrounding region represents an infinite domain around the device. Since an infinite domain cannot be modeled numerically, the domain needs to be truncated at some distance. An important question is then, How large should the surrounding domain be?
To decide how large the surrounding volume must be, one needs to perform a convergence test with respect to the surrounding domain size. In other words, one compares a quantity such as the inductance generated by a coil against the size of the surrounding volume. When the inductance value approaches a steady value, then the domain size no longer needs to be increased. To see the convergence of the value, a simple plot can be created.
In the next example, a convergence test will be performed of the coil model.
As the geometry has an axis of revolution, an axisymmetric simulation can be performed. The model reduces to a 2D model with cylindrical independent variables 
-
. More details about axisymmetric models is found in the Axisymmetric models section.
The 2D version consists in a cross-sectional area of the coil with radius 
. The distance between the 
axis and the coil is 
. The air area surrounding the device is made up of a half-disk of radius 
.
The model is made of an air and a coil region, so to assign different material parameters, region markers are used. Both materials have a relative permeability of 
.
A current of 
[
] will be flowing only through the coil.
At the axis of symmetry, at 
, a zero magnetic vector potential boundary condition is applied.
To perform the convergence test, it is necessary to change the size of the surrounding disk, so in this case, a list of different radius will be defined.
Next, a parametric study will be conducted. The changing parameter is the radius, and as a consequence, there will be a different mesh for each radius. The PDE model will be solved for each radius.
The plot shows that from 
a steady value has been reached.
Boundary Conditions
Boundary conditions for magnetic models fall into one of two categories. One category includes Dirichlet conditions, which specify the magnetic potential at boundaries. In the 
formulation, specifying magnetic potential is equivalent to specifying the normal component of the magnetic flux density. The second category involves boundaries that specify the value of the tangential component of the magnetic field intensity 
. These boundaries are realized with Neumann value boundary conditions.
In addition to these two types of boundary conditions, there is also a third type, known as periodic boundary conditions, which is useful when the geometry has repetitive sections.
For the 
formulation, the following boundary conditions are introduced:
Due to the curl-curl 
nature of the equation, it can be difficult to set up the boundary conditions in 3D. In 2D, the equation simplifies to a diffusion type of equation, and setting the boundary conditions up is much the same as in other PDE model cases. In 3D, specifying boundary conditions for 
often requires specifying the tangential components of 
, 
, or 
. Typically, edge elements or vector elements are used to express the curl-curl nature of the equation. This version of the Wolfram Language does not offer these types of elements. As a consequence, the 3D case is tricky to set up, except for cases where boundaries are parallel to the axes.
In the 
formulation, a boundary condition must be specified for every surface. This is because the automatic finite element–induced Neumann zero value is not useful here. So every surface needs a Dirichlet condition. The details are explained below.
Magnetic Vector Potential Condition
The purpose of a magnetic vector potential boundary condition is to set the tangential components of 
to be equal to the tangential components of a magnetic vector potential 
:
where 
is the outer normal unit vector at the boundary. This is a Dirichlet-type boundary condition.
The magnetic vector potential condition is closely related with a magnetic flux density condition, given by:
Due to the fact that the curl of the vector potential is equal to the magnetic flux density 
:
where 
expresses the tangential components of 
and 
.
The 2D and 3D cases are considered separately.
2D out-of-plane
In the 2D case, there is only one dependent variable 
. This dependent variable is always tangential to the boundaries at the 
-
plane. So, a Dirichlet condition is sufficient to assign a value to 
at a specific boundary.
for the dependent variable 
is modeled with MagneticPotentialCondition:2D axisymmetric out-of-plane
In the 2D-axisymmetric case, there is only one dependent variable 
. This dependent variable is always tangential to the boundaries at the 
-
plane. So, a Dirichlet condition is sufficient to assign a value to 
at a specific boundary. In the 2D-axisymmetric case, the covariant formulation needs to be considered, where 
is substituted by 
:
for the dependent variable 
is modeled with MagneticPotentialCondition:3D
In 3D, there are three dependent variables: 
, 
and 
. The purpose of a magnetic vector potential boundary condition is to set the tangential components of 
to be equal to the tangential components of a magnetic vector potential 
. Here the tangential is computed through the normal 
:
In the current version of the Wolfram Language, the tangential components of a boundary cannot be automatically identified. So for now, the tangential components need to be specified manually. In other words, one specifies a value for each component:
It is easy to identify the tangential components of boundaries that are parallel to one of the coordinate axis. On the other hand, it becomes complicated to specify the tangential component at a boundary that is curved. Edge elements can handle the setup of the tangential components in a more effective manner but are currently not available in the Wolfram Language.
The value for each tangential component needs to be specified individually. For example, at a surface at the boundary at 
, which is a plane parallel to one of the coordinate axes, the tangential components are 
and 
. Using MagneticPotentialCondition, these components can be specified individually.
What may come as a surprise is that MagneticPotentialCondition can be used to specify a magnetic flux.
Magnetic flux
A MagneticPotentialCondition can be used to create a magnetic flux. This is due to the fact that the curl of the vector potential is equal the magnetic flux density 
:
Just like a potential difference in the dependent variable 
generates an electric field, a specific setup of a MagneticPotentialCondition for the components of 
can be used to generate a magnetic field. The magnetic potential condition example shows how to use a magnetic potential condition to set up a homogeneous magnetic field.
Magnetic insulation boundary condition
If the tangential component of 
is set to zero, then a magnetic insulation boundary condition can be modeled with:
This is equivalent to setting the normal component of the magnetic flux density to zero:
A magnetic insulation boundary condition states that there is no magnetic flux across a boundary.
In this formulation, for 2D geometries, a magnetic insulation boundary condition is achieved by specifying a zero value to 
:
where 
is the tangential derivative and 
is the normal component of the magnetic flux density.
Setting the value of 
to zero implies that the normal component 
must vanish at the boundary, since the derivative of a constant is zero.
for the dependent variable 
is modeled with MagneticPotentialCondition:In this formulation, for 2D-axisymmetric geometries, a magnetic insulation boundary condition is achieved by specifying a zero value to 
:
where 
is the tangential derivative and 
is the normal component of the magnetic flux density.
Setting the value of 
to zero implies that the normal component 
must vanish at the boundary, since the derivative of a constant is zero.
for the dependent variable 
is modeled with MagneticPotentialCondition:In 2D-axisymmetric models, at the axis of symmetry, 
, there is no magnetic flux, so a magnetic insulation boundary condition always has to be specified there. That means that at 
, the variable needs to be set to zero, 
.
The setup in 3D needs a bit of thought. Take, for example, a surface boundary that it is in the 
-
plane. A magnetic insulation boundary condition at that boundary will imply that the normal component of the magnetic flux 
at that plane should be zero, 
.
Knowing that 
, to ensure that the normal component 
is zero, 
and 
must be set to zero. Here, 
and 
correspond to the tangential components on the 
-
plane, aligning with the initial equation:
Magnetic symmetry condition
A magnetic symmetry boundary condition is equivalent to an insulation boundary condition. A symmetry boundary condition is used when the computational domain and the magnetic field have mirror symmetry along an axis of the simulation domain.
The symmetry boundary condition is given by:
which states that the normal component of the magnetic flux density is zero. This boundary condition is set up in exactly the same way as an insulation boundary condition.
MagneticPotentialCondition example
The next example will show the use of magnetic potentials at the boundaries and the effects they have. The model consists of an iron cube in a homogeneous magnetic field of 
[
] directed along the 
axis. The model is shown in the figure below, where the gray cube represents the iron cube and the blue arrows the magnetic field. This example is taken from [Mesquita & Bastos, 1992].
On the left: An iron cube inside an homogeneous magnetic field directed in the positive 
axis. On the right: 1/8 of the domain.
The domain is composed of an iron cube of length 
[
] and, due to symmetry, only 1/8 of the whole domain is simulated. The air boundary surrounding the iron cube is another a cube of length 
[
].
The magnetic field is antisymmetric to the 
plane and symmetric to the other planes. These planes are represented as boundaries in the model.
Region markers will be employed to specify the material parameters of the iron and air regions.
The parameters to be used are the permeability of iron 
=1000 and vacuum 
=1.
A magnetic insulation boundary condition is applied at the surface of the boundaries at 
and 
. On these surfaces, the respective tangential components of 
are set to zero.
Then, at the surfaces at 
and 
, the normal component 
is set to zero; this is to only have normal components of the magnetic field at these two surfaces.
Now, to develop the homogenous magnetic field of 
[
] directed along the 
axis, at 
, 
will have the value of 
and 
, and at 
, 
will have the value of 
and 
. All these components are tangential to the surfaces.
To better understand the boundary conditions, visualize the magnetic potential and see how this potential behaves.
The plot shows that the potential has a curl in the counterclockwise direction. This means that this potential produces the magnetic field in the 
direction, according to 
.
Conditions at Material Interfaces
Maxwell's equations are valid for continuous material. However, in electromagnetics, it is common for electric or magnetic fields to be generated in one medium and transmitted to a second medium with different physical properties. The interface between any two materials is a physical discontinuity in materials. The question then is how are Maxwell equations solved in a multimaterial domain.
In the multimaterial case, the electromagnetics field quantities, of course, adhere to the physics at these material interfaces. These interface conditions are not boundary conditions that must be applied but conditions that provide the mathematical legitimacy to use the finite element method to solve the equations.
At a material interface separating two different materials, the following conditions must be satisfied:
where 
[
] is a surface current density deposited at the interface of medium 1 and medium 2. Eqn. 21 can be written as follows:
which means that the normal component of the magnetic flux density is continuous.
On the other hand, the normal component of the magnetic field intensity will not be continuous. To show this, substitute 
:
showing that the normal component of 
must be discontinuous at the interface boundary. Since the permeability in the two materials 
; the only way that 
is true is when fields 
and 
are discontinuous. 
must be discontinuous at the material interface.
Eqn. 22 means that the tangential component of the magnetic field intensity will be discontinuous if a surface current density is placed deliberately at the interface. If not, then the magnetic field intensity will be continuous across the interface:
On the other hand, substituting 
by 
, the following equation is deduced:
For the 
formulation there is an additional interface condition:
Because 
is being solved for, the tangential component of the magnetic potential is always continuous, and thus this condition is automatically fulfilled with the finite element method.
Edge/Vector Elements
Simulating magnetic fields with 3D geometries using the 
formulation has some limitations when using NDSolve. In three dimensions, and only in three dimensions, the challenge lies in solving for the entire magnetic vector potential, maintaining the original form of a curl-curl equation. Such equations typically require specialized treatment for accurate 3D solutions.
While traditional nodal finite elements, such as Lagrange or serendipity elements, suffice in many areas of physics in a finite element analysis, they fall short in electromagnetics. While the previously presented 3D models rely on nodal elements, imposing boundary conditions or satisfying interface conditions across different media may be difficult.
Generally this issue is addressed with a different type of finite element, adept at handling vector equations: edge elements, also known as curl or vector elements. These elements are specifically designed to accommodate the unique boundary conditions and equations inherent in 3D electromagnetic formulations, notably those involving a curl term. Edge elements are currently not implemented in the current version of NDSolve and it is advised to proceed with caution for 3D models of the 
formulation.
For finite element approximations, the 3D 
magnetostatic PDE is multiplied with a test function 
and integrated over:
The integrand 
in the boundary integral is then replaced with a Neumann value. In this way, edge elements handle these types of boundary conditions naturally.
Nomenclature
References
1. Blinder, S. M. (2011, March 7). "Magnetic Hysteresis." Wolfram Demonstrations Project. Retrieved from http://demonstrations.wolfram.com/MagneticHysteresis
2. Cardoso, J. R. (2018). Electromagnetics through the Finite Element Method. Boca Raton: CRC Press.
3. Domke, H.-J. (2011, March 7). "A Simple Model of Magnetization." Wolfram Demonstrations Project. Retrieved from http://demonstrations.wolfram.com/ASimpleModelOfMagnetization
4. Griffiths, D. J. (2017). Introduction to Electrodynamics (4th ed.). Cambridge University Press.
5. Gutfleisch, O., Willard, M. A., Brück, E., Chen, C. H., Sankar, S. G. and Liu, J. P. (2011). "Magnetic Materials and Devices for the 21st Century: Stronger, Lighter, and More Energy Efficient." Advanced Materials, 23(7), pp. 821–842.
6. Ida, N. and Bastos, J. P. (2013). Electromagnetics and Calculation of Fields. Springer Science & Business Media.
7. Jin, J.-M. The Finite Element Method in Electromagnetics. John Wiley & Sons, 2015.
8. Kumar, S. and Tummuru, T. (2016, December). "Jiles–Atherton Model of Magnetic Hysteresis." Wolfram Demonstrations Project. Retrieved from https://demonstrations.wolfram.com/JilesAthertonModelOfMagneticHysteresis
9. Küpfmüller, K. (1968). Einführung in die theoretische Elektrotechnik. Springer.
10. Mesquita, R. C. and Bastos, J. P. A. (1992). "An Incomplete Gauge Formulation for 3D Nodal Finite-Element Magnetostatics." IEEE Transactions on Magnetics, 28(2), pp. 1044–1047.
11. Purcell, E. M. (2013). Electricity and Magnetism. Cambridge University Press.
12. Sadiku, M. N. O. (2011). Elements of Electromagnetics (5th ed.). Oxford University Press.