MagneticPDEComponent
MagneticPDEComponent[vars,pars]
生成带有变量 vars 和 pars 的磁偏微分方程项.
更多信息



- MagneticPDEComponent 生成一个方程,来模拟静磁场和低频电磁场,其模型变量为 vars,模型参数为 pars.
- MagneticPDEComponent 返回微分算子之和,用作偏微分方程的一部分:
- MagneticPDEComponent 模拟由永磁体产生的静磁场或由导电材料中的低频电流产生的磁场和电场.
- MagneticPDEComponent 通常用于模拟电动机、电感器和电磁铁.
- MagneticPDEComponent 创建用于稳态、时间、频率和参数化分析的 PDE 分量.
- MagneticPDEComponent 模拟静磁场学和低频电磁现象,其中,因变量为磁矢量势
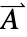 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , "m"}, webers per meter, {{(, "Webers", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , "m"}, webers per meter, {{(, "Webers", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/4.png) ],自变量为
],自变量为 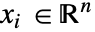 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagneticPDEComponent.zh/6.png) ].
]. - MagneticPDEComponent 也可以模拟静态情况下的外部电流.
- 在静态情况下,没有电流时,应使用 MagnetostaticPDEComponent.
- 值为向量的因变量
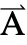 由三个分量组成
由三个分量组成 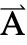 ={Ax1,Ax2,Ax3}.
={Ax1,Ax2,Ax3}. - 稳态变量 vars 为 vars={
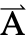 [x1,…,xn],{x1,…,xn}}.
[x1,…,xn],{x1,…,xn}}. - 与频率相关的变量 vars 为 vars={
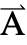 [x1,…,xn],ω,{,…,xn}}.
[x1,…,xn],ω,{,…,xn}}. - 与时间相关的变量 vars 为 vars={
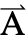 [t,x1,…,xn],t,{x1,…,xn}}.
[t,x1,…,xn],t,{x1,…,xn}}. - MagneticPDEComponent 给出一个稳态磁模型:
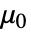 是真空磁导率,单位为 [
是真空磁导率,单位为 [![TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/14.png) ],
],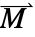 是磁化矢量,单位为 [
是磁化矢量,单位为 [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/16.png) ],
],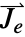 是外部电流密度向量,单位为 [
是外部电流密度向量,单位为 [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/18.png) ].
].- 磁化矢量
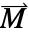 指定材料内每单位体积的磁偶极矩,表明其磁性的强度和方向.
指定材料内每单位体积的磁偶极矩,表明其磁性的强度和方向. - MagneticPDEComponent 给出频域模型:
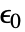 [
[![TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/22.png) ] 是真空介电常数,
] 是真空介电常数,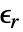 [-] 为相对介电常数,电导率为
[-] 为相对介电常数,电导率为 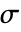 [
[![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/25.png) ],角频率为
],角频率为 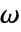 [
[![TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/27.png) ],虚数单位为
],虚数单位为 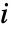 .
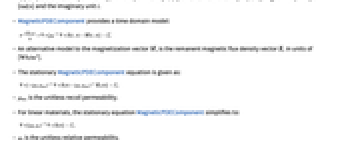
.- MagneticPDEComponent 给出时域模型:
- 磁化矢量
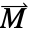 的替代模型为剩余磁通密度向量
的替代模型为剩余磁通密度向量 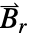 ,单位为 [
,单位为 [![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/32.png) ].
]. - 稳态 MagneticPDEComponent 方程由下式给出:
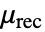 是没有单位的反冲磁导率.
是没有单位的反冲磁导率.- 对于线性材料,稳态方程 MagneticPDEComponent 简化为:
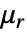 是没有单位的相对磁导率.
是没有单位的相对磁导率.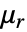 可以是各向同性的、正交各向异性的或各向异性的.
可以是各向同性的、正交各向异性的或各向异性的.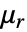 也可以是磁场的函数,描述非线性材料.
也可以是磁场的函数,描述非线性材料.- 磁模型项的单位是 [
![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/39.png) ].
]. - 可给出以下参数 pars:
-
参数 默认值 符号 "ExternalCurrentSource" {0,…} 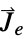 ,外部电流密度向量,单位为 [
,外部电流密度向量,单位为 [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/41.png) ]
]"Magnetization" {0,…} 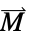 ,磁化矢量,单位为 [
,磁化矢量,单位为 [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/43.png) ]
]"MagneticModelForm" None 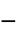
"RegionSymmetry" None 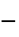
"RelativePermeability" 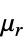 ,相对磁导率,没有单位
,相对磁导率,没有单位
"RemanentMagneticFluxDensity" {0,…} 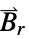 ,剩余磁通密度,单位为 [
,剩余磁通密度,单位为 [![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/48.png) ]
]"Thickness" 1 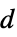 ,厚度,单位为 [
,厚度,单位为 [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagneticPDEComponent.zh/50.png) ]
] "VacuumPermeability" 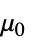
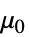 ,真空磁导率,单位为 [
,真空磁导率,单位为 [![TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/53.png) ]
] - 可以为频域和时域模型指定其他参数:
-
参数 默认值 符号 "ElectricalConductivity" 1 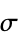 ,电导率,单位为 [
,电导率,单位为 [![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticPDEComponent.zh/55.png) ]
]
- 自变量
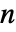 的数量确定了
的数量确定了 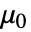 、
、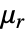 和
和 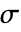 的维数和向量
的维数和向量 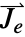 、
、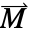 和
和 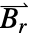 的长度.
的长度. - 该模型有二维、二维轴对称和三维形式.
- 对于相对磁导率
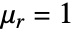 的 3D 稳态模型,可将 "MagneticModelForm" 设为 "FreeSpace",根据库仑规范条件,
的 3D 稳态模型,可将 "MagneticModelForm" 设为 "FreeSpace",根据库仑规范条件, 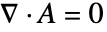 ,3D 算符简化为:
,3D 算符简化为: - 在二维中,磁矢势指向平面外,只有
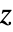 分量. 在稳态线性情况下,该方程由下式给出:
分量. 在稳态线性情况下,该方程由下式给出: 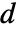 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagneticPDEComponent.zh/69.png) ] 是表示
] 是表示  方向上的 "Thickness" 的变量,因变量
方向上的 "Thickness" 的变量,因变量 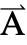 被指定为
被指定为 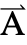 ={0,0,Az}.
={0,0,Az}.- 参数 "RegionSymmetry" 的一个可能选择是 "Axisymmetric".
- "Axisymmetric" 区域对称表示截断圆柱坐标系,其中通过去除角变量来减少圆柱坐标,如下所示:
-
维度 简化 例如:线性稳态方程 2D 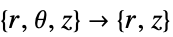
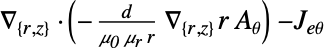
- 为了求解此方程,我们利用了协变公式. 协变公式是一种将变量替换应用于轴对称方程的方法,由
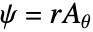 给出:
给出: - 参数的输入指定与其对应的算符完全相同.
- 如果未指定任何参数,则默认磁偏微分方程项为:
- 如果 MagneticPDEComponent 依赖于关联 pars 中以 …,keypi…,pivi,…] 形式指定的参数
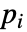 ,则参数
,则参数  将被替换为
将被替换为 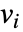 .
.
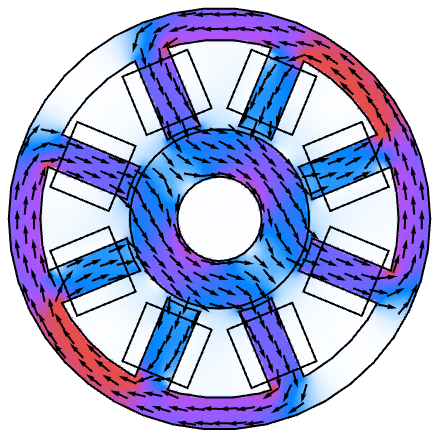
范例
打开所有单元关闭所有单元范围 (7)
定义一个符号二维 out-of-plane 磁 PDE 模型,其真空磁导率为 ![]() ,相对磁导率为
,相对磁导率为 ![]() ,
,![]() 方向上有外部电流:
方向上有外部电流:
定义一个相对磁导率为 1 的 3D 自由空间磁 PDE 模型:
设置默认磁 PDE 模型,其中,真空磁导率为 ![]() ,相对磁导率
,相对磁导率 ![]() ,并保留 Quantity 对象:
,并保留 Quantity 对象:
Wolfram Research (2025),MagneticPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MagneticPDEComponent.html.
文本
Wolfram Research (2025),MagneticPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MagneticPDEComponent.html.
CMS
Wolfram 语言. 2025. "MagneticPDEComponent." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MagneticPDEComponent.html.
APA
Wolfram 语言. (2025). MagneticPDEComponent. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MagneticPDEComponent.html 年