WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

MagneticSymmetryValue

MagneticSymmetryValue[pred,vars,pars]

PDEの磁気対称性境界条件を，適用場所を示す述語 pred，モデル変数 vars，大域パラメータ pars で表す．

MagneticSymmetryValue[pred,vars,pars,lkey]

磁気対称性境界条件を，pars[lkey]で指定された局所パラメータで表す．

詳細

MagneticSymmetryValueはMagnetostaticPDEComponentの対称境界条件を指定する．
MagneticSymmetryValueはMagnetostaticPDEComponentの境界条件を指定するもので，以下のモデリング方程式の一部として使われている．

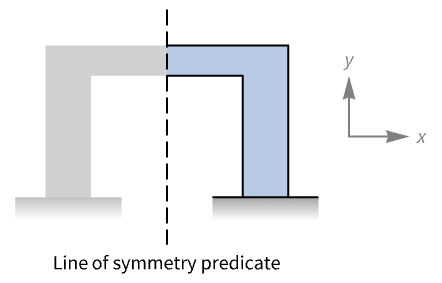
MagneticSymmetryValueは，通常，軸に沿った鏡面対称性を持つ境界をモデル化するために使われる．

MagneticSymmetryValueは，鏡面対称性を持つ境界を，従属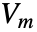変数，独立変数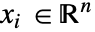でモデル化する．
定常変数 vars は vars={V_m[x₁,…,x_n],{x₁,…,x_n}}である．
真空透磁率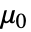（単位：[]），相対透磁率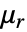のMagnetostaticPDEComponentの線形形式は以下で与えられる．

境界単位法線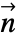および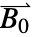を持つMagneticSymmetryValueは，磁束密度ベクトルモデルである．

MagnetostaticPDEComponentに指定されたモデルパラメータ pars．
MagneticSymmetryValueは，事実上，電束が0のMagneticFluxDensityValueと同じである．
境界述語 pred はNeumannValueにおけるのと同じように指定できる．
MagneticSymmetryValueが，連想 pars で…,keyp_i…,p_iv_i,…]として指定されるパラメータに依存するなら，パラメータ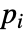は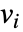で置換される．

例題

すべて開くすべて閉じる

例 (1)

磁気対称性境界条件を設定する：

スコープ (1)

磁気対称性境界条件を3Dで設定する：

アプリケーション (1)

空気中に埋め込まれ，軸に沿ったf []の均一磁場内に出現した鉄の立方体をモデル化しり．領域は長さ []の鉄の立方体で構成される．対称性があるので，領域全体の1/8のみのシミュレーションを行う．鉄の立方体を囲む空気境界は， []の2番目の立方体としてモデル化される．

被約幾何では，- 平面および - 平面に平行な平面には対称境界条件が適用されなければならない．

メッシュを定義する：

メッシュには内部の鉄の立方体を表す内部境界がある．鉄の立方体を定義する：

メッシュのワイヤフレームを定義する：

変数を定義する：

真空の透磁率および鉄の透磁率のパラメータを定義する：

領域全体の均一な磁場を指定するために，の境界に垂直な外向きの磁束密度が指定される．

磁束密度条件を設定する：

磁気対称条件を設定する：

磁気対称条件は，境界上では何も指定されなければデフォルト境界条件であるノイマン(Neumann)0境界条件なので，省略することができる．

静磁気PDEモデルを解く：

磁場の強度を計算する：

場の別の1/8を可視化するために，における場の対称性動作を考えなければならない．の値が正のとき，場はで，の値が負のとき，場はである．

完全幾何ので対称ベクトル場を可視化する：

トップへ