MagneticSymmetryValue[pred,vars,pars]
represents a magnetic symmetry boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MagneticSymmetryValue[pred,vars,pars,lkey]
represents a magnetic symmetry boundary condition with local parameters specified in pars[lkey].


MagneticSymmetryValue
MagneticSymmetryValue[pred,vars,pars]
represents a magnetic symmetry boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MagneticSymmetryValue[pred,vars,pars,lkey]
represents a magnetic symmetry boundary condition with local parameters specified in pars[lkey].
Details


- MagneticSymmetryValue specifies a symmetry boundary condition for MagnetostaticPDEComponent.
- MagneticSymmetryValue specifies a boundary condition for MagnetostaticPDEComponent and is used as part of the modeling equation:
- MagneticSymmetryValue is typically used to model a boundary with mirror symmetry along an axis.
- MagneticSymmetryValue models a boundary with mirror symmetry with dependent variable
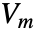 and independent variables
and independent variables 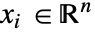 .
. - Stationary variables vars are vars={Vm[x1,…,xn],{x1,…,xn}}.
- The linear form of MagnetostaticPDEComponent with vacuum permeability
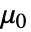 in units of [
in units of [![TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagneticSymmetryValue.en/6.png) ] and relative permeability
] and relative permeability 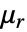 is given by:
is given by: - MagneticSymmetryValue with boundary unit normal
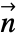 and
and 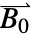 a magnetic flux density vector models:
a magnetic flux density vector models: - Model parameters pars as specified as for MagnetostaticPDEComponent.
- MagneticSymmetryValue is effectively the same as MagneticFluxDensityValue with a magnetic flux of 0.
- The boundary predicate pred can be specified as in NeumannValue.
- If the MagneticSymmetryValue depends on parameters
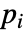 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 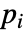 are replaced with
are replaced with 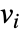 .
.
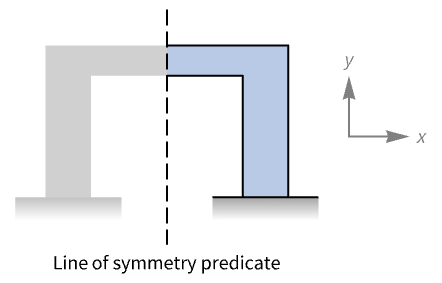
Examples
open all close allScope (2)
Applications (1)
Model an iron cube embedded in air and emerged in a homogeneous magnetic field of ![]() [
[![]() ] directed along the
] directed along the ![]() axis. The domain is composed of an iron cube of length
axis. The domain is composed of an iron cube of length ![]() [
[![]() ]. Due to symmetry, only 1/8 of the whole domain is simulated. The air boundary surrounding the iron cube is modeled as a second cube of length
]. Due to symmetry, only 1/8 of the whole domain is simulated. The air boundary surrounding the iron cube is modeled as a second cube of length ![]() [
[![]() ].
].
In the reduced geometry, at the surfaces parallel to the planes ![]() -
-![]() and
and ![]() -
-![]() a symmetry boundary condition needs to be applied.
a symmetry boundary condition needs to be applied.
The mesh has internal boundaries that represent the inner iron cube. Define the iron cube:
Visualize a wireframe of the mesh:
Define parameters the permeability of vacuum ![]() and iron
and iron ![]() :
:
To specify the homogeneous magnetic field across the domain, an outward magnetic flux density ![]() normal to the boundary at
normal to the boundary at ![]() is specified.
is specified.
Set up the magnetic flux density condition:
Set up the magnetic symmetry condition:
Since the magnetic symmetry condition is a Neumann zero boundary condition, which is the default boundary condition if nothing is specified on a boundary, it could also be omitted.
Solve the magnetostatic PDE model:
Compute the magnetic field intensity:
To visualize another 1/8 of the field, at ![]() , the symmetric behavior of the field must be considered. At positive
, the symmetric behavior of the field must be considered. At positive ![]() values, the field is
values, the field is ![]() and at negative
and at negative ![]() values, the field is
values, the field is ![]() .
.
Visualize the symmetric vector field at ![]() of the complete geometry:
of the complete geometry:
Related Guides
History
Text
Wolfram Research (2025), MagneticSymmetryValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MagneticSymmetryValue.html.
CMS
Wolfram Language. 2025. "MagneticSymmetryValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MagneticSymmetryValue.html.
APA
Wolfram Language. (2025). MagneticSymmetryValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MagneticSymmetryValue.html
BibTeX
@misc{reference.wolfram_2025_magneticsymmetryvalue, author="Wolfram Research", title="{MagneticSymmetryValue}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/MagneticSymmetryValue.html}", note=[Accessed: 05-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_magneticsymmetryvalue, organization={Wolfram Research}, title={MagneticSymmetryValue}, year={2025}, url={https://reference.wolfram.com/language/ref/MagneticSymmetryValue.html}, note=[Accessed: 05-January-2026]}