MatrixGame
MatrixGame[{{![]() ,…},…}]
,…},…}]
プレーヤー1と2がそれぞれ行動 i と j を取る場合のプレーヤー1の利得が ![]() ,プレーヤー2の利得が-
,プレーヤー2の利得が-![]() であるゼロ和二人ゲームを指定する.
であるゼロ和二人ゲームを指定する.
MatrixGame[{{{![]() ,
,![]() },…},…}]
},…},…}]
プレーヤー1と2がそれぞれ行動 i と j を取る場合のプレーヤー1の利得が ![]() ,プレーヤー2の利得が
,プレーヤー2の利得が ![]() である非ゼロ和二人ゲームを指定する.
である非ゼロ和二人ゲームを指定する.
MatrixGame[{…{{![]() ,…,
,…,![]() },…}…}]
},…}…}]
プレーヤー1からプレーヤー n までがそれぞれ行動 i1,…,inを取る場合のプレーヤー k の利得が ![]() である一般的な n 人ゲームを指定する.
である一般的な n 人ゲームを指定する.
詳細とオプション


- MatrixGameは,標準型ゲーム,戦略型ゲーム,同時手番ゲーム,双行列ゲーム,ワンショットゲームとしても知られている.
- MatrixGameは,通常,同時に行動する2人以上のプレーヤーがいる決定問題をモデル化するために使われる.例として,ジャンケンのような手遊びだけでなく,囚人のジレンマや市場ゲームのような軍事ゲームやビジネスゲームもある.
- プレーヤーが2人の行列ゲームは利得ベクトルの配列
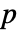 で表現される.プレーヤー1に可能な行動が
で表現される.プレーヤー1に可能な行動が 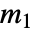 種類,プレーヤー2に可能な行動が
種類,プレーヤー2に可能な行動が 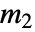 種類の場合,
種類の場合,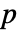 の次元は
の次元は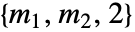 および p〚i,j,k〛==
および p〚i,j,k〛==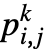 である.
である. 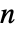 人ゲームは利得ベクトルの深さ
人ゲームは利得ベクトルの深さ 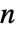 の配列
の配列 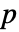 で表される.プレーヤー
で表される.プレーヤー 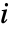 に可能な行動が
に可能な行動が 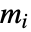 種類なら,
種類なら,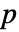 は次元
は次元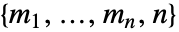 と p〚i1,…,in,k〛==
と p〚i1,…,in,k〛==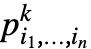 を持つ.
を持つ.- 最適戦略を求めるためにはFindMatrixGameStrategiesを使うとよい.戦略からの期待される利得が求めたければMatrixGamePayoffを使うとよい.
- 次は,使用可能なオプションである.
-
GameActionLabels Automatic 行動に使用するラベル GamePlayerLabels Automatic プレーヤーに使用するラベル - MatrixGameの特性には次の特性が g["prop"]として含まれる.
-
"ComponentPayoffArray" 深さ 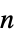 のプレーヤー配列
のプレーヤー配列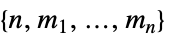 の長さ
の長さ 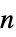 のベクトル
のベクトル"Dataset" プレーヤーのDatasetをタイプセットする "GameActionLabels" 行動ラベルのリスト "GamePlayerLabels" プレーヤーラベルのリスト "PayoffArray" 長さ 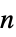 の利得ベクトル
の利得ベクトル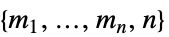 の深さ
の深さ 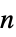 の配列
の配列"Plot" 可視化 "TreeGame" 行列ゲームを木ゲームに変換する - 行列ゲームの指定方法には,主に次元
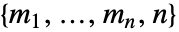 の利得ベクトルの配列"PayoffArray"と次元
の利得ベクトルの配列"PayoffArray"と次元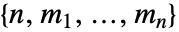 の利得配列のベクトル"ComponentPayoffArray"の2つの形式がある.
の利得配列のベクトル"ComponentPayoffArray"の2つの形式がある.

例題
すべて開くすべて閉じる例 (4)
スコープ (10)
基本的な用法 (3)
特別なゼロ和ゲーム (2)
規則ベースのゲーム (2)
成分配列と複合配列 (2)
MatrixGameを使って成分配列に基づいて複合配列を作成する:
MatrixGameを使って複合配列に基づいて成分配列を作成する:
ゲームの特性 (1)
MatrixGameオブジェクトは,ゲームについての情報を与える特性を含む:
"Properties"特性は,使用可能な特性のリストを与える:
"ObjectType"特性は,ゲームのオブジェクトタイプを与える:
"Summary"特性は,ゲームについての情報の簡単な要約を与える:
"CompositePayoffArray"特性は,ゲームの利得配列の複合形式を与える:
"ComponentPayoffArray"特性は,ゲームの利得配列の成分形式を与える:
"PayoffArray"特性もまた,ゲームの利得配列の成分形式を与える:
"PayoffData"特性は,各プレーヤーの可能な利得のリストを与える:
"Dataset"特性は,行列ゲームを利得のデータ集合として与える:
"Plot"特性は,行列ゲームをMatrixGamePlotと同じ方法でプロットする:
"TreeGame"特性は,任意のMatrixGameをTreeGameに変換する:
オプション (4)
ActionLabels (2)
GamePlayerLabels (2)
これらにはGamePlayerLabelsを介してアクセスできる:
アプリケーション (11)
進化/生物学ゲーム (1)
ワキモンユタトカゲは異なる3つのタイプのオスという繁殖戦略を持つ.喉がオレンジ色のオスは大きいハーレムを持つ.喉が青いオスは維持するメスの数は少ないがこれを守る傾向が強い.喉が黄色のオスはメスの振りをしてハーレムに忍び込む.野外での観察に基づき,それぞれのオスの戦略の適合度は既存のオスの出現頻度に強く依存することが分かっている.![]() は,
は,![]() 番目の戦略を持つオスに支配された環境における
番目の戦略を持つオスに支配された環境における ![]() 番目の戦略の適合度を与える:
番目の戦略の適合度を与える:
適合行列から,ジャンケンと同じようなプレーヤーが2人の対称ゲームが定義できる:
プロットからも分かるように,このゲームはジャンケンに似ている:
混合集団の中で,各戦略の適合度は恋愛ゲームの期待される利得として定義できる:
次世代における各戦略の集団が現世代の集団とその適合度に比例すると仮定すると,次の環境ダイナミクスが与えられる:
余暇のゲーム (3)
ジャンケンは,石 > ハサミ,ハサミ > 紙,紙 > 石の循環順序に基づいている.このゲームを表すグラフを作成する:
グラフを使って支配順を設定することでジャンケン(石-紙-ハサミ)を石-紙-ハサミ-火-水に一般化する:
モラは古代ギリシャや古代ローマの時代から何千年も続くハンドゲームである.各プレーヤーが同時に任意の数の指を出した手を見せ,指の数を言う.全員の指の合計数を言い当てたプレーヤーがポイントを得る.
スポーツゲーム (1)
経済ゲーム (3)
腹をすかせた3人の男がレストランに行って会計を割り勘にすることにした.定食には高いものと安いものの2つのオプションがある.安い方の値段は良心的な10ドルで高い方は40ドル相当のものに50ドルの値段がついている.この状況をMatrixGameとして表現する:
価格戦争は,複数の企業が最低価格を提供しようとするが任意の企業の利得が選択される価格に直接相関することである.3つの企業間の価格戦争について考える.各企業は低価格か高価格を選ぶことができる:
価格をできるだけ高くするという共通の利害があるにもかかわらず,競争によって低価格でナッシュ均衡が生まれる:
一組の夫婦がアクティビティA,B,Cから選べるとする.妻はAを,夫はBを好むが,どちらもCは好まない.この状況をMatrixGameを使って表す:
軍事ゲーム (1)
ブロット大佐ゲームは2人のプレーヤーが同時にいくつかの戦場に限られた中隊を分配するゼロ和ゲームである.戦場ごとに最も多くの中隊を届けたプレーヤーがその戦闘に勝つ.利得は勝利を収めた戦場数である.戦場数が2で,ブロット大佐側は2隊,敵側は4隊のブロット大佐ゲームについて考える:
交通ゲーム (2)
2人のプレーヤーが同じ時間に同じ交差点に到着する.どちらのプレーヤーも直進するか止まるかできる.両方が直進すると,結果は死亡事故になる.直進に成功した場合の利得は1,停止した場合の利得は0である.この状況をMatrixGameとして表す:
これを見ると,一般に.死亡事故を除外する戦略がナッシュ均衡であることがわかる:
驚くべきことに,道路網に1つまたは複数の道路を追加すると全体的な交通が遅くなる可能性がある.これはブライスのパラドックスとして知られるものである.a から b までの道路網がある場合,c または d を介して2つの異なる道路網を使用するとする.道路 ac と db は20 n 分かかる.ここで,n は道路上のドライバーの数である.cb と ad はドライバーの数には関係なく45分かかる.道路網をグラフとして表す:
ドライバーの数を n=2として,a から b へのすべての経路を求める:
全部で4通りの経路があるが,各経路を選択したドライバーの数を数える:
通勤者が選択した異なる経路に対応する2つの純粋な戦略がある:
上記の交通ゲームを追いながら,モデリングを自動化し一般的な道路網を解く.ここで,start 頂点と end 頂点は車の出発点と到達点であり,道路の各部分の容量は辺重みを使って符号化されている:
この状況は2人のドライバーのための新たな交通ゲームを定義する:
既存2つの経路間で切り替えると,唯一の安定解では通勤時間は制限された道路網(65分)よりも長く(82分)なるという囚人のジレンマのような状態になる:
考えられる問題 (1)
与えられた配列が完全配列でなければ,MatrixGameは評価されない:
テキスト
Wolfram Research (2025), MatrixGame, Wolfram言語関数, https://reference.wolfram.com/language/ref/MatrixGame.html.
CMS
Wolfram Language. 2025. "MatrixGame." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixGame.html.
APA
Wolfram Language. (2025). MatrixGame. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixGame.html

