MatrixGame[{{![]() ,…},…}]
,…},…}]
specifies a zero-sum two-player game with payoff ![]() for player 1 and -
for player 1 and -![]() for player 2 when players 1 and 2 take actions i and j, respectively.
for player 2 when players 1 and 2 take actions i and j, respectively.
MatrixGame[{{{![]() ,
,![]() },…},…}]
},…},…}]
specifies a general-sum two-player game with payoff ![]() for player 1 and
for player 1 and ![]() for player 2 when players 1 and 2 take actions i and j, respectively.
for player 2 when players 1 and 2 take actions i and j, respectively.
MatrixGame[{…{{![]() ,…,
,…,![]() },…}…}]
},…}…}]
specifies a general n-player game with payoff ![]() for player k when players 1 through n take actions i1,…,in, respectively.
for player k when players 1 through n take actions i1,…,in, respectively.


MatrixGame
MatrixGame[{{![]() ,…},…}]
,…},…}]
specifies a zero-sum two-player game with payoff ![]() for player 1 and -
for player 1 and -![]() for player 2 when players 1 and 2 take actions i and j, respectively.
for player 2 when players 1 and 2 take actions i and j, respectively.
MatrixGame[{{{![]() ,
,![]() },…},…}]
},…},…}]
specifies a general-sum two-player game with payoff ![]() for player 1 and
for player 1 and ![]() for player 2 when players 1 and 2 take actions i and j, respectively.
for player 2 when players 1 and 2 take actions i and j, respectively.
MatrixGame[{…{{![]() ,…,
,…,![]() },…}…}]
},…}…}]
specifies a general n-player game with payoff ![]() for player k when players 1 through n take actions i1,…,in, respectively.
for player k when players 1 through n take actions i1,…,in, respectively.
Details and Options


- MatrixGame is also known as normal form game, strategic form game, simultaneous move game, bimatrix game and one-shot game.
- MatrixGame is typically used to model decision problems with two or more players acting simultaneously. Examples include hand games such as Rock Paper Scissors, but also military and business games such as Prisoner's Dilemma and market games.
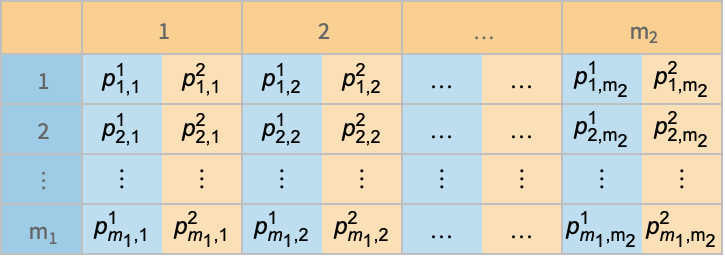
- A two-player game is described by an array
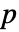 of payoff vectors. If player 1 has
of payoff vectors. If player 1 has  possible actions and player 2 has
possible actions and player 2 has 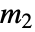 possible actions, then
possible actions, then 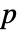 has dimensions
has dimensions 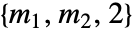 and p〚i,j,k〛==
and p〚i,j,k〛==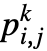 .
. - An
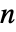 -player game is described by a depth
-player game is described by a depth 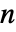 array
array 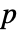 of payoff vectors. If player
of payoff vectors. If player 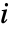 has
has 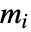 possible actions, then
possible actions, then 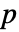 has dimensions
has dimensions 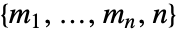 and p〚i1,…,in,k〛==
and p〚i1,…,in,k〛==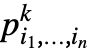 .
. - To find an optimal strategy, use FindMatrixGameStrategies. To find the expected payoff from a strategy, use MatrixGamePayoff.
- The following options can be given:
-
GameActionLabels Automatic labels to use for actions GamePlayerLabels Automatic labels to use for players - Properties for MatrixGame include the following properties as g["prop"]:
-
"ComponentPayoffArray" length 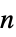 vector of depth-
vector of depth-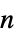 player arrays
player arrays 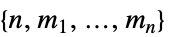
"Dataset" typeset Dataset of payoffs "GameActionLabels" list of action labels "GamePlayerLabels" list of player labels "PayoffArray" depth- 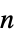 array of length-
array of length-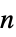 payoff vectors
payoff vectors 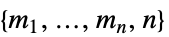
"Plot" visualization "TreeGame" convert a matrix game to a tree game - There are two main forms to specify a matrix game, namely as an array of payoff vectors "PayoffArray" with dimensions
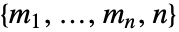 or as a vector of payoff arrays "ComponentPayoffArray" with dimensions
or as a vector of payoff arrays "ComponentPayoffArray" with dimensions 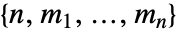 .
.
Examples
open all close allBasic Examples (4)
Scope (10)
Basic Uses (3)
Special Zero-Sum Games (2)
Rule-Based Games (2)
Component and Composite Arrays (2)
Manually create a composite array based on a component array:
Create a composite array based on a component array using MatrixGame:
Manually create a component array based on a composite array:
Create a component array based on a composite array using MatrixGame:
Game Properties (1)
MatrixGame objects include properties that give information about the game:
The "Properties" property gives a list of properties available:
The "ObjectType" property gives the object type of the game:
The "Summary" property gives a brief summary of information about the game:
The "CompositePayoffArray" property gives the composite form of the payoff array of the game:
The "ComponentPayoffArray" property gives the component form of the payoff array of the game:
The "PayoffArray" property also gives the component form of the payoff array of the game:
The "PayoffData" property gives the list of possible payoffs for each player:
The "Dataset" property gives the matrix game as a dataset of payoffs:
The "Plot" property plots the matrix game in the same fashion as MatrixGamePlot:
The "TreeGame" property converts any MatrixGame into a TreeGame:
Options (4)
GameActionLabels (2)
Specify the names of the actions of each player:
These can be accessed through GameActionLabels:
This changes the result from the "Dataset" property:
Consider a random game about the yield of vegetables starting with "p":
Note if the wrong number of action labels is provided, they will be ignored:
GamePlayerLabels (2)
Specify the names of the actions of each player:
These can be accessed through GamePlayerLabels:
Consider a random game about the yield of vegetables for three farmers:
View the plot and note that the tooltips of the figure were based on the player labels:
Applications (11)
Evolutionary/Biological Games (1)
The common side-blotched lizards have three distinct male mating strategies. The orange-necked ones maintain large harems, the blue-necked ones keep fewer females but are more protective, and the yellow-necked ones pretend to be females and can sneak into harems. Based on field observations, the fitness of each individual male strategy is known, which strongly depends on the already-present males' frequencies. ![]() gives the fitness of the
gives the fitness of the ![]() strategy in an environment dominated by males with the
strategy in an environment dominated by males with the ![]() strategy:
strategy:
Assuming the game is symmetric, find the component payoff array:
Define a symmetric two-player game:
This game is similar to Rock Paper Scissors, as can be seen from their plots:
In a mixed population, the fitness of each strategy can be determined as the expected payoff of the mating game:
Assuming that the population of each strategy in the next generation is proportional to the current population and its fitness yields the following evolutionary dynamics:
Starting from 35% yellow-, 50% blue- and 15% orange-necked lizards, an oscillatory pattern can be observed in the first 100 generations:
The oscillation may be avoided when starting at the Nash equilibrium:
Recreational Games (3)
Rock Paper Scissors is based on a cyclic order rock>scissors, scissors>paper, paper>rock. Create the graph representation of this game:
Create the game using the graph representation:
Generalize Rock Paper Scissors to Rock Paper Scissors Fire Water by setting up a dominance order using a graph:
Create the whole game as a zero-sum game:
Morra is a hand game that dates back thousands of years to ancient Roman and Greek times. Each player simultaneously reveals their hand, extending any number of fingers, and calls out a number. Any player who successfully guesses the total number of fingers revealed by all players combined scores a point.
A two-player, "m-finger" Morra game can be constructed in the following way:
A traditional five-finger Morra is a symmetric zero-sum game with 50 available actions for both players:
Sports Games (1)
In various games, including soccer, baseball and tennis, players face decisions where no predetermined action is optimal. For example, in soccer during penalty kicks, both the kicker and the goalkeeper should randomize if they kick/move to the right or the left. Because of missed kicks and other errors, the scoring probabilities can vary. Based on real-world data, a realistic scoring matrix looks like the following:
An obvious question is how the kicker and the goalkeeper should randomize their strategies:
And the scoring frequencies in this case:
One can carry out the same computations when the scoring probabilities are changed:
Interestingly, the conventional wisdom to "prioritize your strong side" is not optimal in most of the cases:
Economics Games (3)
Three hungry men go to a restaurant and decide to split the bill evenly. There are two meal options, Cheap and Expensive. The Cheap meal is fairly priced at $10, while the Expensive meal would be fairly priced at $40 but is overpriced at $50. Represent this situation as a MatrixGame:
A price war refers to a game where multiple firms have an interest in offering the lowest price, but the payoff of any firm is directly correlated to the price chosen. Consider a price war between three firms where each firm has the choice between a low price and a high price:
Despite the common interest of having the price as high as possible, competition creates a Nash equilibrium at the low price:
A couple can choose from activities A, B, C. The wife prefers A, the husband B, and neither of them likes C. Represent the situation using a MatrixGame:
Military Games (1)
The Colonel Blotto game is a two-person zero-sum game in which the players are tasked to simultaneously distribute limited troops over several battlefields. The player devoting the most troops to a battlefield wins that battlefield, and the payoff is equal to the total number of battlefields won. Consider a Colonel Blotto game with two battlefields where Colonel Blotto has 2 units and Enemy has 4 units:
Traffic Games (2)
Two players drive up to the same intersection at the same time. Each player can either cross or stop. If both attempt to cross, the result is a fatal accident. Successfully crossing has a payoff of 1, and stopping has a payoff of 0. Represent this situation as a MatrixGame:
Generally, strategies excluding the fatal accident are Nash equilibria:
Amazingly, adding one or more roads to a road network can slow overall traffic, known as Braess's paradox. Given a road network from a to b, take two different paths either via c or d. The roads ac and db take 20 n minutes, where n is the number of drivers on the road; cb and ad take 45 minutes independent of the number of drivers. Represent the road network as a graph:
For two drivers n=2, find all paths from a to b:
Count the number of drivers for each choice of path, which gives four cases:
Find the total the time taken for each case:
Maximize the negative commute time:
Create the traffic game based on the payoff matrix:
The two pure strategies correspond to the commuters picking different paths:
Those pure strategies also give the shortest commute time of 65 minutes:
Following the traffic game above, the modeling and solving for a general road network can be automated. Here start and end are start and end vertices, and each road segment capacity is encoded using edge weight:
Add a short high-capacity road segment between d and c:
This situation defines a new traffic game for two drivers:
The new possibility of switching between the two previously existing routes resulted in a Prisoner's Dilemma–like situation, where the only stable solution results in a longer commuting time (82 minutes), compared to the restricted network (65 minutes):
Possible Issues (1)
MatrixGame does not evaluate if one of the arrays given is not a full array:
Neat Examples (1)
The payoffs in this game are: a Hawk meeting a Dove gets the highest payoff (3), but if they meet another Hawk, they both get the lowest payoff (0). A Dove meeting a Hawk gets 1, and when two Doves meet, they both get 2.
Form a payoff simulation function of the Hawk-Dove game:
At the end of each time step, after all individuals have played the game, one randomly selected player from each population revises their strategy—Hawk or Dove—according to the following rule: "I look at another (randomly selected) individual in my population; if and only if they got a payoff higher than mine, I adopt their strategy". Create the intrapopulation Imitation Model visualization:
Related Guides
History
Text
Wolfram Research (2025), MatrixGame, Wolfram Language function, https://reference.wolfram.com/language/ref/MatrixGame.html.
CMS
Wolfram Language. 2025. "MatrixGame." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixGame.html.
APA
Wolfram Language. (2025). MatrixGame. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixGame.html
BibTeX
@misc{reference.wolfram_2025_matrixgame, author="Wolfram Research", title="{MatrixGame}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/MatrixGame.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_matrixgame, organization={Wolfram Research}, title={MatrixGame}, year={2025}, url={https://reference.wolfram.com/language/ref/MatrixGame.html}, note=[Accessed: 24-February-2026]}

