WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

MersennePrimeExponent

MersennePrimeExponent[n]

n 番目のメルセンヌ(Mersenne)素数指数を与える．

詳細

メルセンヌ素数指数は，メルセンヌ数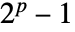が素数となる素数 p である．
MersennePrimeExponent[n]では，n は正の整数でなければならない．
Wolfram言語の現行バージョンの時点では，最初の48個のメルセンヌ素数指数までが確定的な順位を持つ．後3個のメルセンヌ素数指数が知られているが，その順位は未知のままである．MersennePrimeExponent[n]は，48より大きい n のメルセンヌ素数指数を求めようとするが，適当な時間内に結果が返されることは期待できない．

例題

すべて開くすべて閉じる

例 (1)

最初の10個のメルセンヌ素数指数を返す：

対応するメルセンヌ素数を構築する：

そのすべてが素数かどうかをチェックする：

スコープ (1)

MersennePrimeExponentは自動的にリストに縫い込まれる：

特性と関係 (5)

メルセンヌ素数指数は偶完全数を生成する：

メルセンヌ素数の三角数は偶数の完全数を生成する：

メルセンヌ素数指数に関連する六角数は偶数の完全数を生成する：

メルセンヌ素数指数は超完全数を生成する：

次数がメルセンヌ素数指数である三項式は，それが既約であるときかつそのときに限り2を法とした原始多項式である：

考えられる問題 (1)

Wolfram言語の現行バージョンの時点では，順序が定まっているメルセンヌ素数指数は48個だけである：

さらに3つのメルセンヌ素数指数が知られているが，その順序はまだ未知である：

トップへ