MersennePrimeExponentQ
Details
- MersennePrimeExponentQ is typically used to test whether an integer is a Mersenne prime exponent.
- A positive integer n is a Mersenne prime exponent if the Mersenne number
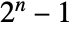 is prime.
is prime. - MersennePrimeExponentQ[n] returns False unless n is manifestly a Mersenne prime exponent.
Examples
open all close allBasic Examples (2)
Scope (3)
MersennePrimeExponentQ works over integers:
Applications (8)
Basic Applications (3)
Special Sequences (2)
Number Theory (3)
Properties & Relations (10)
Mersenne prime exponents are prime numbers:
Composite numbers cannot be MersennePrimeExponents:
The only even Mersenne prime exponent is ![]() :
:
MersennePrimeExponent gives the ![]()
![]() Mersenne prime exponent:
Mersenne prime exponent:
![]() is a Mersenne prime, where p is a Mersenne prime exponent:
is a Mersenne prime, where p is a Mersenne prime exponent:
If p is a Mersenne prime exponent, then ![]() is a perfect number:
is a perfect number:
Every even perfect number has the form ![]() , where p is a Mersenne prime exponent:
, where p is a Mersenne prime exponent:
Check that in the representation above p is 5:
Triangular numbers of Mersenne primes are perfect numbers:
Hexagonal numbers related to Mersenne prime exponents are perfect numbers:
Possible Issues (2)
Expressions that represent Mersenne prime exponents but do not evaluate explicitly will give False:
It is necessary to use symbolic simplification first:
As of this version of the Wolfram Language, only 49 Mersenne prime exponents have definite ranking:
Three more Mersenne prime exponents are known, but their ranking is still unknown:
Related Guides
History
Text
Wolfram Research (2016), MersennePrimeExponentQ, Wolfram Language function, https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html.
CMS
Wolfram Language. 2016. "MersennePrimeExponentQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html.
APA
Wolfram Language. (2016). MersennePrimeExponentQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html
BibTeX
@misc{reference.wolfram_2025_mersenneprimeexponentq, author="Wolfram Research", title="{MersennePrimeExponentQ}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_mersenneprimeexponentq, organization={Wolfram Research}, title={MersennePrimeExponentQ}, year={2016}, url={https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html}, note=[Accessed: 17-January-2026]}

