MersennePrimeExponent

MersennePrimeExponent[n]

给出第 n 个梅森素数指数.

更多信息

  • 梅森素数指数是使得梅森数 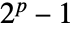为素数的素数 p.
  • 在 MersennePrimeExponent[n] 中，n 必须为正整数.
  • 在这个版本的 Wolfram 语言中，只有 48 个梅森素数指数有明确的排名. 另外还有三个梅森素数指数已知，但尚不清楚它们的排名. MersennePrimeExponent[n] 将尝试寻找 n 大于 48 的梅森素数指数，但可能无法在合理的时间内返回结果.

范例

打开所有单元关闭所有单元

基本范例  (1)

返回前十个梅森素数指数：

构造相应的梅森素数：

验证这些都是素数：

范围  (1)

MersennePrimeExponent 自动遍历列表中的各项：

属性和关系  (5)

梅森素数指数生成偶完全数：

梅森素数的三角形数生成偶完美数：

与梅森素数指数相关的六角形数生成偶完美数：

梅森素数指数生成超完美数：

次数为梅森素数指数的三项式是本原多项式模 2 的条件是当且仅当它是不可约的：

可能存在的问题  (1)

到本版本的 Wolfram 语言为止，只有 48 个梅森素数指数有确定的排名：

目前又找到了三个梅森素数指数，但它们的排名依然未知：

Wolfram Research (2016)，MersennePrimeExponent，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MersennePrimeExponent.html （更新于 2024 年）.

文本

Wolfram Research (2016)，MersennePrimeExponent，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MersennePrimeExponent.html （更新于 2024 年）.

CMS

Wolfram 语言. 2016. "MersennePrimeExponent." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/MersennePrimeExponent.html.

APA

Wolfram 语言. (2016). MersennePrimeExponent. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MersennePrimeExponent.html 年

BibTeX

@misc{reference.wolfram_2024_mersenneprimeexponent, author="Wolfram Research", title="{MersennePrimeExponent}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/MersennePrimeExponent.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mersenneprimeexponent, organization={Wolfram Research}, title={MersennePrimeExponent}, year={2024}, url={https://reference.wolfram.com/language/ref/MersennePrimeExponent.html}, note=[Accessed: 21-November-2024 ]}