MonsterGroupM
表示散在 monster 单群 ![]() .
.
背景
- MonsterGroupM[] 表示魔群
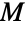 ,是阶数为
,是阶数为 ![TemplateBox[{2, 46}, Superscript].TemplateBox[{3, 20}, Superscript].TemplateBox[{5, 9}, Superscript].TemplateBox[{7, 6}, Superscript].TemplateBox[{11, 2}, Superscript].TemplateBox[{13, 3}, Superscript].17.19.23.29.31.41.47.59.71 TemplateBox[{2, 46}, Superscript].TemplateBox[{3, 20}, Superscript].TemplateBox[{5, 9}, Superscript].TemplateBox[{7, 6}, Superscript].TemplateBox[{11, 2}, Superscript].TemplateBox[{13, 3}, Superscript].17.19.23.29.31.41.47.59.71](Files/MonsterGroupM.zh/3.png) 的群. 是 26 个散在有限单群之一.
的群. 是 26 个散在有限单群之一. - 魔群
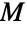 是最大的散在有限单群. 在二十世纪七十年代早期,数学家 Bernd Fischer 推测该群作为单群存在,并含有小魔群作为对合的中心化子. 尽管许多数学家在二十世纪七十年代对魔群做了大量的研究,但直到 Griess 在二十世纪八十年代早期明确构建了
是最大的散在有限单群. 在二十世纪七十年代早期,数学家 Bernd Fischer 推测该群作为单群存在,并含有小魔群作为对合的中心化子. 尽管许多数学家在二十世纪七十年代对魔群做了大量的研究,但直到 Griess 在二十世纪八十年代早期明确构建了 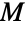 ,它的存在才被确认. 魔群有一个在两个元素的场
,它的存在才被确认. 魔群有一个在两个元素的场 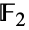 上的维数为
上的维数为 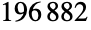 的忠实线性表示,以及在
的忠实线性表示,以及在 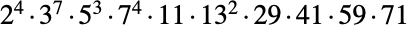 个点上的忠实置换表示. 它是有理数上的一个 Galois 群、一个 Hurwitz 群和所谓的怪兽顶点代数的自同构群. 与其他散在单群一起,魔群在有限单群的重要(和完全)分类中发挥了基础性作用.
个点上的忠实置换表示. 它是有理数上的一个 Galois 群、一个 Hurwitz 群和所谓的怪兽顶点代数的自同构群. 与其他散在单群一起,魔群在有限单群的重要(和完全)分类中发挥了基础性作用. - 常见的群论函数都可用于 MonsterGroupM[],包括 GroupOrder、GroupGenerators、GroupElements 等等. 然而,尽管 MonsterGroupM[] 是一个置换群,由于它的阶数较大,明确的置换表示对于直接实现是不切实际的. 所以,在应用有些群论函数时,可能以未计算的形式返回. 可通过 FiniteGroupData["Monster","prop"] 获取一些已预先算好的魔群的属性.
- MonsterGroupM 与其他一些符号有关. MonsterGroupM 是被称作“第三代”的八个(与 FischerGroupFi22、FischerGroupFi23、FischerGroupFi24Prime、HeldGroupHe、HaradaNortonGroupHN、BabyMonsterGroupB 和 ThompsonGroupTh 一起)散在有限单群之一. MonsterGroupM 的子商包含了除六个散在群(所谓的“贱民”)之外的所有散在群.
相关指南
-
▪
- 已命名的群
文本
Wolfram Research (2010),MonsterGroupM,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MonsterGroupM.html.
CMS
Wolfram 语言. 2010. "MonsterGroupM." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MonsterGroupM.html.
APA
Wolfram 语言. (2010). MonsterGroupM. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MonsterGroupM.html 年
BibTeX
@misc{reference.wolfram_2025_monstergroupm, author="Wolfram Research", title="{MonsterGroupM}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MonsterGroupM.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_monstergroupm, organization={Wolfram Research}, title={MonsterGroupM}, year={2010}, url={https://reference.wolfram.com/language/ref/MonsterGroupM.html}, note=[Accessed: 07-February-2026]}

