MultiplicativeOrder

MultiplicativeOrder[k,n]

n を法とした kの乗法的位数を与え， であるような最小の整数 として定義される．

MultiplicativeOrder[k,n,{r1,r2,…}]

n を法とした k の一般化された乗法的位数を与え，任意の に対して であるような最小の整数 として定義される．

詳細

  • MultiplicativeOrderはモジュロ位数あるいはハウプト指数としても知られている．
  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • モジュラー演算や暗号学でよく使われる．
  • MultiplicativeOrder[k,n]は，kmを n で割った余りが1と等しい最小の正の整数 m を与える．
  • MultiplicativeOrderは，必要条件を満たす整数 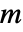が存在しない場合，結果は評価されない．
  • FiniteFieldElementオブジェクト a について，MultiplicativeOrder[a]は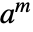，が乗法の単位元となるような，有限体の最小の正の整数 m と定義される a の乗法的位数を与える．

例題

すべて開くすべて閉じる

例  (2)

8を法とした5の乗法的位数：

法を固定して数列をプロットする：

法を変えながら数列をプロットする：

スコープ  (7)

数値評価  (5)

整数を使って計算する：

一般化された乗法的位数：

大きい数を使って計算する：

有限体の元の乗法的位数：

TraditionalFormによる表示：

記号演算  (2)

Solveを使って方程式の解を求める：

FindInstanceを使って解を求める：

アプリケーション  (9)

基本的なアプリケーション  (5)

43を法とした原始根を求める：

が素数で10が の原始根であるとき，有理数 は長さ で桁が循環する：

NestWhileListを使ってMultiplicativeOrderを計算する：

与えられた素数を法としたときの可能な乗法的位数の数を数える：

が素数のときの の除数の数：

両者は同じリストである：

整数論  (4)

奇数 についてのルールの反復周期は q[n]を分割する：

を基数としたの桁は周期で繰り返される：

関数digitCycleLengthは， を基数とした任意の有理数 についての桁周期を与える：

次は，10を基数としたの小数表現が3桁周期で繰り返されることを示している：

RSAのようなトイ暗号スキームを構築する：

循環攻撃を行う．出力の1つはテキストである：

特性と関係  (5)

n を法とする原始根の乗法的位数はEulerPhi[n]である：

EulerPhiはMultiplicativeOrderを割る：

結果は常に正である：

≡ 2, 3あるいは7を法とした4になるよう最小の整数を求める：

どの余りがを満足するかを求める：

で離散対数問題を解く：

考えられる問題  (1)

非零の整数 k と n について，k と n が互いに素のときかつその時に限りMultiplicativeOrder[k,n]が存在する：

しかし，10と22は互いに素ではない：

インタラクティブな例題  (1)

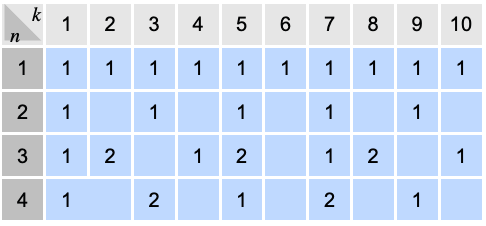
指定された素数より小さい各整数のMultiplicativeOrder：

おもしろい例題  (2)

ある数がいつ12を法として乗法的位数を持つかを可視化する：

MultiplicativeOrderのウラム(Ulam)螺線：

Wolfram Research (1999), MultiplicativeOrder, Wolfram言語関数， https://reference.wolfram.com/language/ref/MultiplicativeOrder.html （2023年に更新）.

テキスト

Wolfram Research (1999), MultiplicativeOrder, Wolfram言語関数， https://reference.wolfram.com/language/ref/MultiplicativeOrder.html （2023年に更新）.

CMS

Wolfram Language. 1999. "MultiplicativeOrder." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/MultiplicativeOrder.html.

APA

Wolfram Language. (1999). MultiplicativeOrder. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultiplicativeOrder.html

BibTeX

@misc{reference.wolfram_2024_multiplicativeorder, author="Wolfram Research", title="{MultiplicativeOrder}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/MultiplicativeOrder.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_multiplicativeorder, organization={Wolfram Research}, title={MultiplicativeOrder}, year={2023}, url={https://reference.wolfram.com/language/ref/MultiplicativeOrder.html}, note=[Accessed: 05-November-2024 ]}