PIDTune
PIDTune[sys]
線形時不変系 sys のフィードバックPID制御器を与える.
PIDTune[sys,"carch"]
アーキテクチャ"carch"("P","PI","PID"等)の制御器を与える.
PIDTune[sys,{"carch","trule"}]
調整規則"trule"を使って制御器を与える.
PIDTune[sys,…,"prop"]
特性"prop"の値を与える.
詳細とオプション




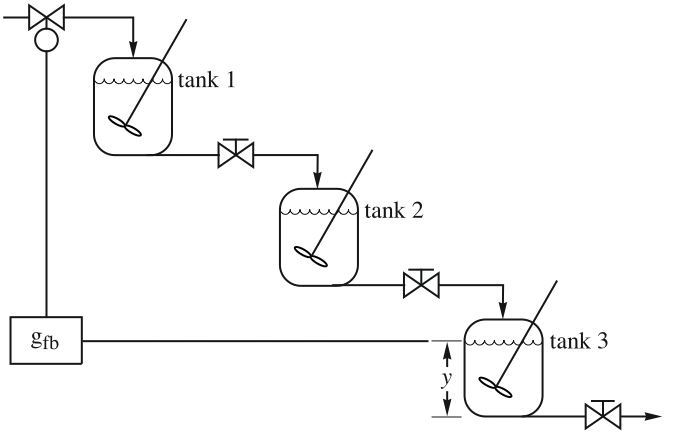
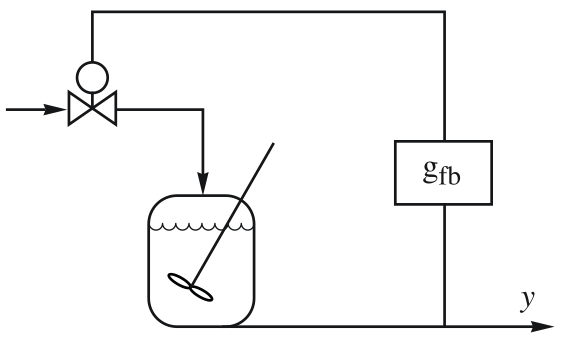
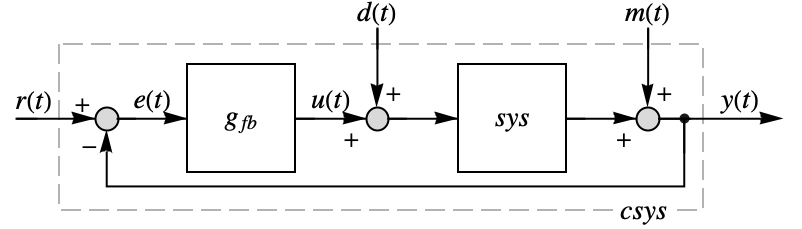
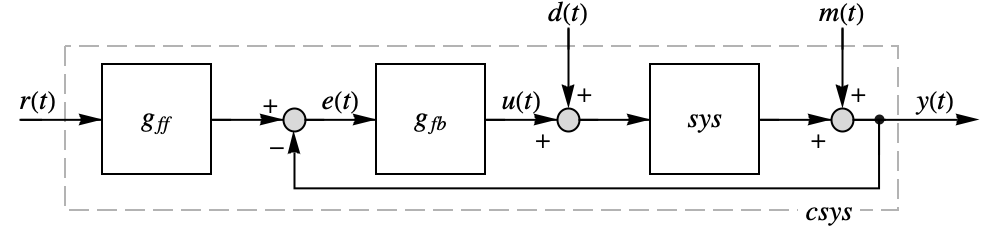
- PIDTuneは,閉ループ系 csys が外乱
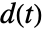 を拒絶し基準
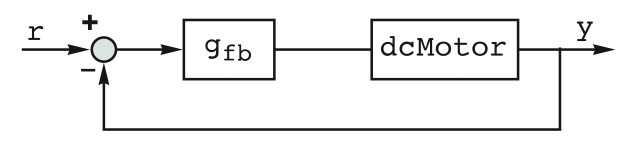
を拒絶し基準 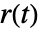 の変化に従うことができるような,PID制御器 gfbを作成する.
の変化に従うことができるような,PID制御器 gfbを作成する. - 理想的なPID制御器は,事実上,比例,積分,微分の各項がある
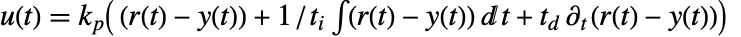 によって制御信号
によって制御信号 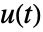 を計算する.
を計算する. - デフォルトで,gfbを表す伝達関数が返される.
- 系 sys は以下の単一入力単一出力(SISO)の連続時間系のいずれでもよい.
-
TransferFunctionModel[…] 入出力周波数領域モデル StateSpaceModel[…] 線形制御入力と線形状態 AffineStateSpaceModel[…] 線形制御入力と非線形状態 NonlinearStateSpaceModel[…] 非線形制御入力と非線形状態 SystemModel[…] 一般的な系のモデル - AffineStateSpaceModel,NonlinearStateSpaceModel,SystemModelのような非線形系については,系は保存された動作点の周りで線形化される.
- PIDTuneはSISOコントローラ設計技術である.PIDTune[sspec,…]を使って複数入力複数出力系のSISO部分系が指定できる.
- 系の指定 sspec は次のキーを持つAssociationである.
-
"InputModel" 入力モデル sys "FeedbackInput" sys のフィードバック入力 "MeasuredOutput" sys の測定された出力 - 次の制御器アーキテクチャ"carch"を使うことができる.
-
"P" 比例 "PI" 比例積分 "PD" 比例微分 "PID" 比例積分微分 "PFD" フィルタされた微分部分がある"PD" "PIFD" フィルタされた微分部分がある"PID" - デフォルトで,"PI"制御器が選ばれる.
- 明示的な指定がない限り,系 sys の安定性特性に基づいて,調整規則"trule"が自動的に選ばれる.
- 使用可能な"trule"規則
-
"AMIGO" 近似 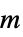 制約積分ゲイン最適化
制約積分ゲイン最適化"AMIGOFrequency" 周波数応答からの"AMIGO" "ChienHronesReswick" ステップ応答に基づいた規則を使う "CohenCoon" 割合0.25での振幅減衰のための支配極設置 "DisturbanceRejection" 外乱応答の無限ノルムの最小化 "ErrorIntegral" 誤差 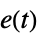 の積分の最小化
の積分の最小化"KappaTau" 支配極設置 "KappaTauFrequency" 周波数応答からの支配極設置 "LambdaTuning" 内部モデル制御を使う "LoopShaping" 厳密な"AMIGO" "SkogestadIMC" 半規則削減に基づいた内部モード制御を使う "TyreusLuyben" 周波数応答に基づいた規則を使う "ZieglerNichols" ステップ応答に基づいた規則を使う "ZieglerNicholsFrequency" 周波数応答に基づいた規則を使う - PIDTune[sys,…,"Data"]はSystemsModelControllerDataオブジェクト cd を返す.これを使って cd["prop"]の形で追加的な特性が抽出できる.
- PIDTune[sys,…,"prop"]を使って cd["prop"]の値を直接与えることができる.
- PIDTuneは,フィードバック制御器 gfbの外乱拒絶機能とは独立に,基準
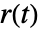 の追跡を向上させるためにフィードフォワードフィルタgffをオプションで計算することができる.
の追跡を向上させるためにフィードフォワードフィルタgffをオプションで計算することができる. - フィードフォワード重み b および c はPID制御器の異なる項に供給される基準信号
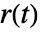 の割合に影響を与える.結果の制御器は,事実上
の割合に影響を与える.結果の制御器は,事実上 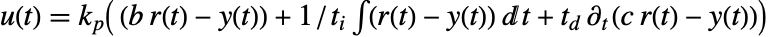 で与えられるが,フィードバック制御器 gfbと組み合されたときに同じ効果を持つような別個のフィードフォワードフィルタ gffとして与えられる.
で与えられるが,フィードバック制御器 gfbと組み合されたときに同じ効果を持つような別個のフィードフォワードフィルタ gffとして与えられる. - さまざまな伝達関数に関連する特性
-
"Feedback" フィードバック gfb "Feedforward" フィードフォワード gff "OpenLoop" gfb および lsys の直列接続 "DisturbanceOutput" 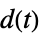 から
から 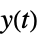 への伝達関数
への伝達関数"DisturbanceControl" 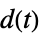 から
から 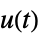 への伝達関数
への伝達関数"ReferenceOutput" 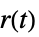 から
から 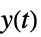 への伝達関数
への伝達関数"ReferenceControl" 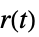 から
から 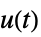 への伝達関数
への伝達関数"SensorOutput" 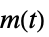 から
から 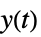 への伝達関数
への伝達関数"SensorControl" 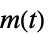 から
から 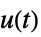 への伝達関数
への伝達関数"ISA" 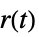 および
および 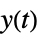 から
から 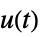 への伝達関数
への伝達関数"ClosedLoop" 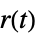 ,
, 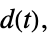
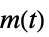 から
から 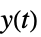 への伝達関数
への伝達関数 - 伝達関数のパラメータ化に関連する特性
-
"FeedbackIdealParameters" 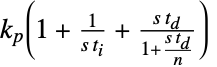 中の{kp,ti,td}
中の{kp,ti,td}"FeedbackSeriesParameters" 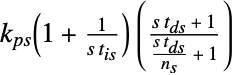 中の{kps,tis,tds}
中の{kps,tis,tds}"FeedbackParallelParameters" 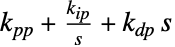 中の{kpp,kip,kdp}
中の{kpp,kip,kdp}"FeedforwardParameters" gff 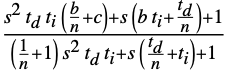 中の{b,c}
中の{b,c}"DerivativeFilterParameter" gff および gfb中の n 個の制御微分フィルタ - 微分フィルタは直接微分
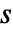 をそのフィルタにかけたもの
をそのフィルタにかけたもの 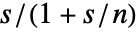 で置換し,事実上微分とローパスフィルタを直列接続する.
で置換し,事実上微分とローパスフィルタを直列接続する. - sys の調整規則と内部調整モデルに関連する特性
-
"TuningRule" 選択された調整規則 "TuningModel" モデルとパラメータ{"tmodel",{par1,…}} - 可能な調整モデルとパラメータ
-
{"FOPTD2",{kv,l}} 一次プラス時間遅延 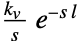
{"FOPTD3",{ks,l,tc} 一次プラス時間遅延 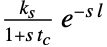
{"Frequency2",{ku,tu}} 最終ゲインと最終周期 {"Frequency3",{ku,tu,ks} 最終ゲイン,最終周期,静的ゲイン {"SOPTD",{ks,l,tc1,tc2}} 二次プラス時間遅延 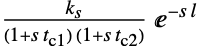
- パラメータは静的ゲイン
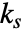 ,速度定数
,速度定数 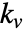 ,遅延
,遅延 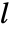 ,時間定数
,時間定数 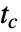 ,最終ゲイン
,最終ゲイン 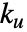 ,最終周期
,最終周期 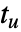 である.
である. - 使用可能なオプション
-
PIDFeedforward None gffの基準重み PIDDerivativeFilter None フィルタされた微分 Method Automatic 使用するメソッド - Methodの設定で調整モデルを導くパラメータ推定メソッドを制御する.
- Methodの可能な設定値
-
Automatic 推定メソッドを自動的に選択する "CharacteristicArea" ステップ応答の指標領域を使う "GainMargins" 位相交差周波数とゲイン余裕を使う "InflectionPoint" ステップ応答の変曲点を使う "MethodOfMoments" モーメントをマッチする "TwoPointSampling" ステップ応答の28%点および63%点を使う
例題
すべて開くすべて閉じるスコープ (17)
基本的な用法 (4)
特性 (4)
SystemsModelControllerDataオブジェクトを入手し,そこから特性を抽出する:
計算された制御器,PIDフィードバック制御器.フィードフォワードフィルタを求める:
基準,過程外乱,センサーノイズから出力への閉ループ伝達関数を得る:
出力伝達関数に対する外乱は,過程の外乱を拒絶する能力を測る:
出力伝達関数に対するセンサーノイズは,測定ノイズを拒絶する能力を測る:
基準,過程外乱,センサーノイズからコントロール出力への伝達関数を求める:
コントロール伝達関数に対する基準は,基準に従うコントロールの努力を測る:
制御器のアーキテクチャ (4)
調整規則 (5)
オプション (4)
PIDFeedforward (2)
これは,ステップ基準入力への大きいオーバーシュートになることがある:
PIDFeedforwardオプションを使ってトラッキングのパフォーマンスを向上させる:
アプリケーション (4)
特性と関係 (2)
テキスト
Wolfram Research (2012), PIDTune, Wolfram言語関数, https://reference.wolfram.com/language/ref/PIDTune.html (2021年に更新).
CMS
Wolfram Language. 2012. "PIDTune." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/PIDTune.html.
APA
Wolfram Language. (2012). PIDTune. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PIDTune.html