PIDTune
PIDTune[sys]
对线性时不变系统 sys 给出 PID 反馈控制器.
PIDTune[sys,"carch"]
给出结构为 "carch"("P"、"PI"、"PID" 等)的控制器.
PIDTune[sys,{"carch","trule"}]
给出整定规则为 "trule" 的控制器.
PIDTune[sys,…,"prop"]
返回属性 "prop" 的值.
更多信息和选项




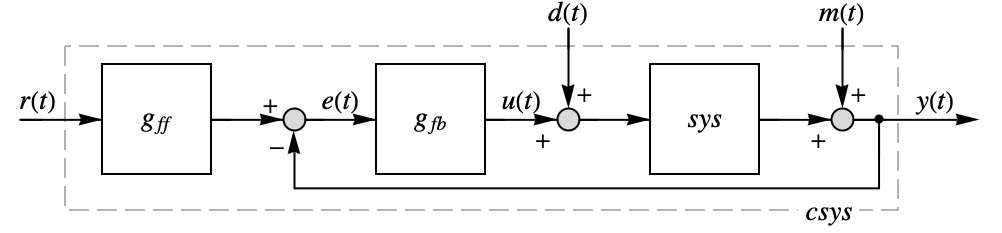
- PIDTune 将产生一个 PID 控制器 gfb,以使闭环系统 csys 具有良好的抵抗扰动
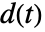 的性能,并能更好地跟随参考信号
的性能,并能更好地跟随参考信号 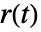 的变化.
的变化. - 理想 PID 控制器利用比例单元、积分单元和微分单元,通过
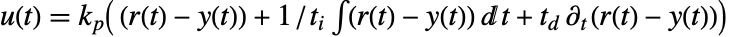 来计算控制信号
来计算控制信号 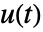 .
. - 默认情况下,返回表示 gfb 的传递函数.
- 系统 sys 可以是以下任何单输入单输出 (SISO) 连续时间系统:
-
TransferFunctionModel[…] 输入输出频域模型 StateSpaceModel[…] 线性控制输入和线性状态 AffineStateSpaceModel[…] 线性控制输入和非线性状态 NonlinearStateSpaceModel[…] 非线性控制输入和非线性状态 SystemModel[…] 一般系统模型 - 对于 AffineStateSpaceModel、NonlinearStateSpaceModel 和 SystemModel 等非线性系统,系统将围绕其存储的工作点进行线性化.
- PIDTune 是一种 SISO 控制器设计技术. PIDTune[sspec,…] 可用于指定多输入多输出系统的 SISO 子系统.
- 系统规范 sspec 是一个 Association,可以具有以下键:
-
"InputModel" 输入模型 sys "FeedbackInput" sys 的反馈输入 "MeasuredOutput" sys 的测量输出 - 可以使用下列控制器结构 "carch":
-
"P" 比例 "PI" 比例积分 "PD" 比例微分 "PID" 比例积分微分 "PFD" 带有滤波微分单元的 "PD" "PIFD" 带有滤波微分单元的 "PID" - 默认情况下,选择 "PI" 控制器.
- 除非明确指定,基于系统 sys 的稳定性,自动选择整定规则 "trule".
- 可以使用下列整定规则 "trule":
-
"AMIGO" 近似  约束积分增益最优化
约束积分增益最优化"AMIGOFrequency" 来自频率响应的 "AMIGO" "ChienHronesReswick" 使用基于阶跃响应的规则 "CohenCoon" 幅值衰减率 0.25 下的主导极点位置 "DisturbanceRejection" 最小化扰动响应的无穷范数 "ErrorIntegral" 最小化误差  的积分
的积分"KappaTau" 主导极点位置 "KappaTauFrequency" 来自频率响应的主导极点位置 "LambdaTuning" 使用内部模型控制 "LoopShaping" 精确 "AMIGO" "SkogestadIMC" 使用基于半规则化简的内部模型控制 "TyreusLuyben" 使用基于频率响应的规则 "ZieglerNichols" 使用基于阶跃响应的规则 "ZieglerNicholsFrequency" 使用基于频率响应的规则 - PIDTune[sys,…,"Data"] 返回一个 SystemsModelControllerData 对象 cd,可用于使用 cd["prop"] 形式提取其他属性.
- PIDTune[sys,…,"prop"] 可用于直接给出 cd["prop"] 的值.
- PIDTune 可以计算前馈滤波器 gff 来改善参考
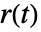 的跟踪,与反馈控制器 gfb 的扰动拒绝功能无关.
的跟踪,与反馈控制器 gfb 的扰动拒绝功能无关. - 前馈权重 b 和 c 影响参考信号
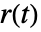 的百分比被提供给 PID 控制器的不同项. 所得控制器由
的百分比被提供给 PID 控制器的不同项. 所得控制器由 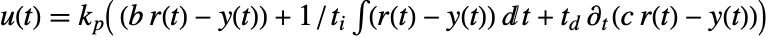 给出,但是作为不同的前馈滤波器 gff 提供时域反馈控制器 gfb 合用有相同的效果.
给出,但是作为不同的前馈滤波器 gff 提供时域反馈控制器 gfb 合用有相同的效果. - 与不同传递函数相关的属性包括:
-
"Feedback" 反馈 gfb "Feedforward" 前馈 gff "OpenLoop" gfb 和 sys 的串联 "DisturbanceOutput" 从 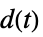 到
到 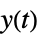 的传递函数
的传递函数"DisturbanceControl" 从 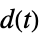 到
到 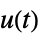 的传递函数
的传递函数"ReferenceOutput" 从  到
到  的传递函数
的传递函数"ReferenceControl" 从  到
到 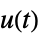 的传递函数
的传递函数"SensorOutput" 从 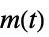 到
到 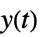 的传递函数
的传递函数"SensorControl" 从 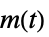 到
到 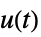 的传递函数
的传递函数"ISA" 从 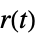 和
和  到
到  的传递函数
的传递函数"ClosedLoop" 从 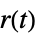 、
、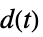 和
和  到
到 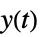 的传递函数
的传递函数 - 与传递函数参数化相关的属性:
-
"FeedbackIdealParameters" {kp,ti,td} 在  中
中"FeedbackSeriesParameters" {kps,tis,tds} 在 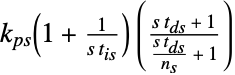 中
中"FeedbackParallelParameters" {kpp,kip,kdp} 在 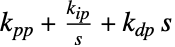 中
中"FeedforwardParameters" {b,c} 在 gff  中
中"DerivativeFilterParameter" 用于控制 gff 和 gfb 中微分滤波器的 n - 微分滤波器将直接微分
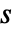 替换为它的滤波版本
替换为它的滤波版本 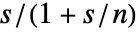 ,实际上相当于将低通滤波器与微分单元串联起来.
,实际上相当于将低通滤波器与微分单元串联起来. - 对于 sys,与整定规则和内部整定模型相关的属性为:
-
"TuningRule" 选中的整定规则 "TuningModel" 模型和参数 {"tmodel",{par1,…}} - 可能的整定模型与参数:
-
{"FOPTD2",{kv,l}} 一阶加纯滞后 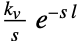
{"FOPTD3",{ks,l,tc} 一阶加纯滞后 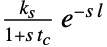
{"Frequency2",{ku,tu}} 极限增益和极限周期 {"Frequency3",{ku,tu,ks} 极限增益、极限周期和静态增益 {"SOPTD",{ks,l,tc1,tc2}} 二阶加纯滞后 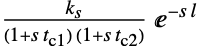
- 参数是静态增益
 、速度常量
、速度常量 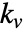 、延迟
、延迟 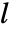 、时间常量
、时间常量  、极限增益
、极限增益 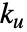 和极限周期
和极限周期  .
. - 可以给出下列选项:
-
PIDFeedforward None gff 的基准权值 PIDDerivativeFilter None 滤波微分器 Method Automatic 所使用的方法 - Method 的设置用于控制推导整定模型的参数估计方法.
- Method 的可能设置包括:
-
Automatic 自动选择估计方法 "CharacteristicArea" 使用阶跃响应的特征区域 "GainMargins" 使用相位交叉频率和增益裕值 "InflectionPoint" 使用阶跃响应的发射点 "MethodOfMoments" 匹配矩 "TwoPointSampling" 使用阶跃响应的 28% 和 63% 点

范例
打开所有单元关闭所有单元范围 (17)
基本用途 (4)
属性 (4)
获取 SystemsModelControllerData 对象并从中提取一个属性:
分别给出从参考信号、过程干扰信号和传感器噪声到输出的闭环传递函数:
分别给出从参考信号、过程干扰信号和传感器噪声到控制信号输出的闭环传递函数:
参考信号到控制信号输出的传递函数表明为跟随参考信号所做的工作量:
控制器结构 (4)
选项 (4)
PIDFeedforward (2)
应用 (4)
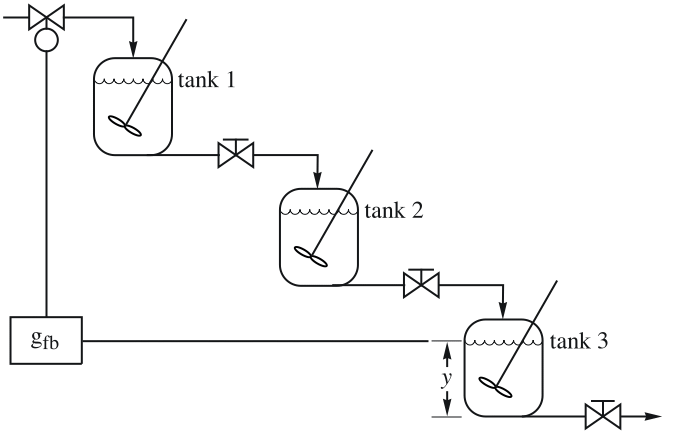
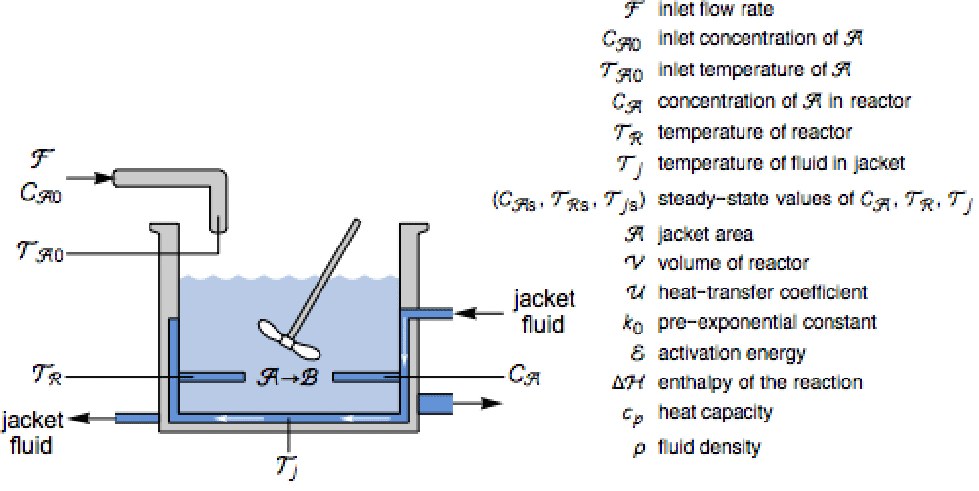
过程控制 (2)
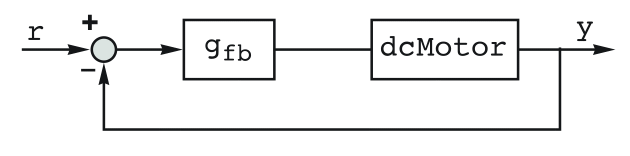
电机控制 (1)
非线性系统控制 (1)
属性和关系 (2)
Wolfram Research (2012),PIDTune,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PIDTune.html (更新于 2021 年).
文本
Wolfram Research (2012),PIDTune,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PIDTune.html (更新于 2021 年).
CMS
Wolfram 语言. 2012. "PIDTune." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/PIDTune.html.
APA
Wolfram 语言. (2012). PIDTune. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PIDTune.html 年