PascalBinomial

PascalBinomial[n,m]

gives the binomial coefficient TemplateBox[{n, m}, PascalBinomial] that preserves Pascal's identity.

Details

  • Integer mathematical function, suitable for both symbolic and numerical manipulation.
  • PascalBinomial is also known as combinations and as choose function.
  • PascalBinomial gives the asymmetric coefficients that preserve Pascal's identity for all integer values. Use Binomial for coefficients that are symmetric for negative integer 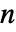. PascalBinomial and Binomial agree except for negative integer .
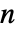  • In general, TemplateBox[{n, m}, PascalBinomial] is defined by (n!)/(m!(n-m)!)=(TemplateBox[{{n, +, 1}}, Gamma])/(TemplateBox[{{m, +, 1}}, Gamma] TemplateBox[{{n, -, m, +, 1}}, Gamma]) or suitable limits of this.
  • When 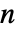is a negative integer, TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{TemplateBox[{{{(, TemplateBox[{{nu, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{mu, +, 1}}, Gamma], , TemplateBox[{{{-, mu}, +, nu, +, 1}}, Gamma]}, )}}, mu, m}, Limit2Arg], nu, n}, Limit2Arg]. »
  • The particular limit chosen preserves Pascal's identity TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{{n, -, 1}, m}, PascalBinomial]+TemplateBox[{{n, -, 1}, {m, -, 1}}, PascalBinomial] for all complex 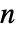and . »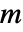
  • The symmetry rule TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{n, {n, -, m}}, PascalBinomial] is satisfied for all 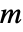and most 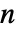but violated for negative integer . »
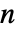  • For integer arguments, PascalBinomial automatically evaluates to exact values.
  • PascalBinomial is automatically evaluated symbolically for simple cases; FunctionExpand gives results for other cases. »
  • PascalBinomial can be evaluated to arbitrary numerical precision.
  • PascalBinomial automatically threads over lists.
  • PascalBinomial can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (5)

Evaluate numerically:

Evaluate symbolically:

Construct Pascal's triangle:

Plot over a subset of the reals as a function of its first parameter:

Plot over a subset of the reals as a function of its second parameter:

Plot over a subset of the complexes:

Scope  (36)

Numerical Evaluation  (7)

Evaluate numerically:

Evaluate for half-integer arguments:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Or compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix PascalBinomial function using MatrixFunction:

Specific Values  (5)

Values of PascalBinomial at particular points:

PascalBinomial for symbolic n:

Values at zero:

Note that this is zero on all integers away from :

PascalBinomial[n,m] is zero whenever n and m are both negative integers:

Find a value of n for which PascalBinomial[n,2]=15:

Visualization  (3)

Plot the PascalBinomial as a function of its parameter n:

Plot the PascalBinomial as a function of its parameter :

Plot the real part of TemplateBox[{z, 5}, PascalBinomial]:

Plot the imaginary part of TemplateBox[{z, 5}, PascalBinomial]:

Function Properties  (12)

Real domain of PascalBinomial as a function of its parameter n:

Real domain of PascalBinomial as a function of its parameter m:

Complex domain:

Function range of PascalBinomial:

PascalBinomial has the mirror property TemplateBox[{TemplateBox[{z}, Conjugate, SyntaxForm -> SuperscriptBox], 2}, PascalBinomial]=TemplateBox[{TemplateBox[{z, 2}, PascalBinomial]}, Conjugate]:

Compute sums involving PascalBinomial:

When is positive, TemplateBox[{x, y}, PascalBinomial] is an analytic function of both variables:

This is not true for negative :

TemplateBox[{x, 7}, PascalBinomial] is neither non-decreasing nor non-increasing:

TemplateBox[{x, 7}, PascalBinomial] is not injective:

TemplateBox[{x, 7}, PascalBinomial] is surjective:

PascalBinomial is neither non-negative nor non-positive:

TemplateBox[{x, y}, PascalBinomial] has singularities and discontinuities where is a negative integer:

TemplateBox[{x, 7}, Binomial] is neither convex nor concave:

TraditionalForm formatting:

Differentiation  (3)

First derivative with respect to :

Higher derivatives with respect to :

Plot the higher derivatives with respect to for :

First derivative with respect to :

Series Expansions  (4)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

Find the series expansion at Infinity:

Find series expansion for an arbitrary symbolic direction :

Taylor expansion at a generic point:

Function Identities and Simplifications  (2)

Functional identity:

Recurrence relations:

Applications  (9)

There are TemplateBox[{n, m}, Binomial] ways to choose elements without replacements from a set of elements:

Check with direct enumeration:

There are TemplateBox[{{m, +, n, -, 1}, m}, Binomial] ways to choose elements with replacement from a set of elements:

Check with direct enumeration:

There are TemplateBox[{{m, +, n}, m}, Binomial] ways to arrange indistinguishable objects of one kind and indistinguishable objects of another kind:

Illustrate the binomial theorem:

Fractional binomial theorem:

Binomial coefficients mod 2:

Plot PascalBinomial in the arguments' plane:

Plot the logarithm of the number of ways to pick elements out of :

Compute higher derivatives of a product of two functions:

Properties & Relations  (8)

On the integers, PascalBinomial[n,m] equals TemplateBox[{TemplateBox[{{{(, TemplateBox[{{nu, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{mu, +, 1}}, Gamma], , TemplateBox[{{{-, mu}, +, nu, +, 1}}, Gamma]}, )}}, mu, m}, Limit2Arg], nu, n}, Limit2Arg]:

This can be expressed as (-1)^m TemplateBox[{{-, n}, m}, Pochhammer]/m! for and otherwise:

An alternative formula on the integers:

Pascal's identity is satisfied everywhere:

In particular, it is true at the origin:

The symmetry rule TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{n, {n, -, m}}, PascalBinomial] may not hold for negative integer :

It may hold for some values but will generally be violated for positive integer :

Binomial satisfies the symmetry rule everywhere:

PascalBinomial performs simple evaluations for symbolic arguments:

PascalBinomial typically does not evaluate when both arguments are symbolic:

Use FunctionExpand with conditions to achieve appropriate simplifications:

PascalBinomial[n,m] is 0 whenever n and m are both negative integers:

Use FullSimplify to simplify expressions involving binomial coefficients:

Use FunctionExpand to expand into Gamma functions:

Sums involving PascalBinomial:

Neat Examples  (7)

Construct a graphical version of Pascal's triangle:

Extend the triangle to negative integers; unlabeled points indicate a zero value:

Binomial, by contrast, defines the top-left sector by reflecting the top-right sector:

Binomial coefficient mod :

Closed‐form inverse of Hilbert matrices:

Nested binomials over the complex plane:

Plot PascalBinomial at infinity:

Plot PascalBinomial for complex arguments:

Plot PascalBinomial at Gaussian integers:

Wolfram Research (2024), PascalBinomial, Wolfram Language function, https://reference.wolfram.com/language/ref/PascalBinomial.html.

Text

Wolfram Research (2024), PascalBinomial, Wolfram Language function, https://reference.wolfram.com/language/ref/PascalBinomial.html.

CMS

Wolfram Language. 2024. "PascalBinomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PascalBinomial.html.

APA

Wolfram Language. (2024). PascalBinomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PascalBinomial.html

BibTeX

@misc{reference.wolfram_2024_pascalbinomial, author="Wolfram Research", title="{PascalBinomial}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PascalBinomial.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pascalbinomial, organization={Wolfram Research}, title={PascalBinomial}, year={2024}, url={https://reference.wolfram.com/language/ref/PascalBinomial.html}, note=[Accessed: 21-December-2024 ]}