PascalBinomial
PascalBinomial[n,m]
パスカル(Pascal)の恒等式を保持する二項係数![]() を与える.
を与える.
詳細

- 記号操作・数値操作の両方に適した数学的整数関数である.
- PascalBinomialは,組合せおよび選択関数としても知られている.
- PascalBinomialは,すべての整数値についてパスカルの恒等式を保持する非対称係数を与える.負の整数
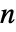 に対して対称である係数にBinomialを使う.PascalBinomialとBinomialは,負の整数
に対して対称である係数にBinomialを使う.PascalBinomialとBinomialは,負の整数 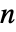 についての場合を除いて一致する.
についての場合を除いて一致する. - 一般に,
![TemplateBox[{n, m}, PascalBinomial] TemplateBox[{n, m}, PascalBinomial]](Files/PascalBinomial.ja/4.png) は,
は,![(n!)/(m!(n-m)!)=(TemplateBox[{{n, +, 1}}, Gamma])/(TemplateBox[{{m, +, 1}}, Gamma] TemplateBox[{{n, -, m, +, 1}}, Gamma]) (n!)/(m!(n-m)!)=(TemplateBox[{{n, +, 1}}, Gamma])/(TemplateBox[{{m, +, 1}}, Gamma] TemplateBox[{{n, -, m, +, 1}}, Gamma])](Files/PascalBinomial.ja/5.png) またはこの適切な極限によって定義される.
またはこの適切な極限によって定義される. 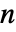 が負の整数のときは,
が負の整数のときは,![TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{TemplateBox[{{{(, TemplateBox[{{nu, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{mu, +, 1}}, Gamma], , TemplateBox[{{{-, mu}, +, nu, +, 1}}, Gamma]}, )}}, mu, m}, Limit2Arg], nu, n}, Limit2Arg] TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{TemplateBox[{{{(, TemplateBox[{{nu, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{mu, +, 1}}, Gamma], , TemplateBox[{{{-, mu}, +, nu, +, 1}}, Gamma]}, )}}, mu, m}, Limit2Arg], nu, n}, Limit2Arg]](Files/PascalBinomial.ja/7.png) である. »
である. »- 選択された特定の極限が,すべての複素数
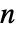 と
と 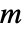 についてパスカルの恒等式
についてパスカルの恒等式![TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{{n, -, 1}, m}, PascalBinomial]+TemplateBox[{{n, -, 1}, {m, -, 1}}, PascalBinomial] TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{{n, -, 1}, m}, PascalBinomial]+TemplateBox[{{n, -, 1}, {m, -, 1}}, PascalBinomial]](Files/PascalBinomial.ja/10.png) を保持する. »
を保持する. » - 対称則
![TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{n, {n, -, m}}, PascalBinomial] TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{n, {n, -, m}}, PascalBinomial]](Files/PascalBinomial.ja/11.png) は,すべての
は,すべての 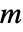 とほとんどの
とほとんどの 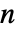 について満足されるが,負の整数
について満足されるが,負の整数 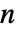 については満足されない. »
については満足されない. » - 整数の引数については,PascalBinomialは自動的に厳密値に評価される.
- PascalBinomialは,単純な場合は自動的に記号的に評価される.その他の場合についてはFunctionExpandが結果を与える. »
- PascalBinomialは任意の数値精度で評価できる.
- PascalBinomialは自動的にリストに縫い込まれる.
- PascalBinomialは,IntervalオブジェクトやCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開くすべて閉じる例 (5)
スコープ (36)
数値評価 (7)
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合の保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のPascalBinomial関数を計算することもできる:
特定の値 (5)
特定の点におけるPascalBinomialの値:
記号的な n についてのPascalBinomial:
n と m が両方とも負の整数のとき,PascalBinomial[n,m]は0である:
PascalBinomial[n,2]=15である n の値を求める:
可視化 (3)
関数の特性 (12)
パラメータ n の関数としてのPascalBinomialの実領域:
パラメータ m の関数としてのPascalBinomialの実領域:
PascalBinomial関数の値域:
PascalBinomialは鏡面特性![]() を持つ:
を持つ:
PascalBinomialを含む和を計算する:
PascalBinomialは,非負でも非正でもない:
TraditionalFormによる表示:
級数展開 (4)
アプリケーション (9)
![]() 個の要素の集合から置換なしで
個の要素の集合から置換なしで ![]() 個の要素を選ぶ方法は
個の要素を選ぶ方法は![]() 通りある:
通りある:
![]() 個の要素の集合から置換ありで
個の要素の集合から置換ありで ![]() 個の要素を選ぶ方法は
個の要素を選ぶ方法は ![]() 通りある:
通りある:
ある種類の区別が付かない ![]() 個のオブジェクトと別の種類の区別が付かない
個のオブジェクトと別の種類の区別が付かない ![]() 個のオブジェクトを並べる方法は
個のオブジェクトを並べる方法は![]() 通りある:
通りある:
引数平面でPascalBinomialをプロットする:
特性と関係 (8)
整数については,PascalBinomial[n,m]は![]() に等しい:
に等しい:
これは,![]() のときは
のときは![]() と表すことができる.それ以外の場合は
と表すことができる.それ以外の場合は![]() である:
である:
値によっては成り立つかもしれないが,一般に正の整数 ![]() の場合は成り立たない:
の場合は成り立たない:
Binomialはあらゆるところで対称則を満足する:
PascalBinomialは,記号引数については単純な評価を行う:
PascalBinomialは,通常,引数が記号のときは評価されない:
FunctionExpandを条件付きで使って適切な簡約を得る:
n と m の両方が負の整数のとき,PascalBinomial[n,m]は0である:
FullSimplifyを使って二項係数を含む式を簡約する:
FunctionExpandを使ってGamma関数に展開する:
PascalBinomialを含む和:
おもしろい例題 (7)
三角形を負の整数に拡張する.ラベルのない点は値0を示している:
一方,Binomialは右上の部分を反映して左上の部分を定義する:
無限大でPascalBinomialをプロットする:
複素係数についてPascalBinomialをプロットする:
ガウス整数でPascalBinomialをプロットする:
テキスト
Wolfram Research (2024), PascalBinomial, Wolfram言語関数, https://reference.wolfram.com/language/ref/PascalBinomial.html.
CMS
Wolfram Language. 2024. "PascalBinomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PascalBinomial.html.
APA
Wolfram Language. (2024). PascalBinomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PascalBinomial.html