Wolfram Language & System Documentation Center

PolynomialHermiteDecomposition

computes the Hermite decomposition of the matrix P of univariate polynomials.

PolynomialHermiteDecomposition[P,x]

computes the Hermite decomposition for a matrix of polynomials in the variable x.

Details

PolynomialHermiteDecomposition is the polynomial analog of HermiteDecomposition. It gives a canonical decomposition of a polynomial matrix as a unimodular and an upper triangular matrix.
PolynomialHermiteDecomposition is typically used in applications similar to where one uses RowReduce with the big difference being that one is only looking for polynomial solutions and not rational function solutions.
The Hermite decomposition is computed by doing polynomial row operations: multiply by a polynomial, permute rows and add rows. This corresponds to multiplying by a matrix 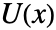from the left, and the result is an upper triangular Hermite form .
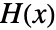The matrix 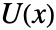is unimodular, i.e. is constant, so the inverse $U^~(x)=TemplateBox[{{U, (, x, )}}, Inverse]$ is also a polynomial matrix. and the polynomial matrix 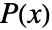has the decomposition :
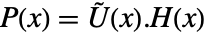The matrix 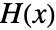is an upper triangular polynomial matrix that is also a canonical form of 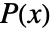up to multiplying each row with constants. The first nonzero entry in each row is a polynomial such that all entries above it are of strictly lower degree and all entries below it are zero.

Examples

open all close all

Basic Examples (2)

Compute the Hermite decomposition of a 2x2 matrix:

Check the matrix equation:

Check that u is unimodular:

Compute the Hermite decomposition of a 2x3 matrix of low-degree polynomials:

Check the matrix equation:

Check that u is unimodular:

Scope (4)

The matrix can have rational coefficients:

Check that the determinant of u is constant and check the required matrix equation:

The matrix can have complex coefficients:

Check that the determinant of u is constant and verify the required matrix equation:

The matrix can have approximate coefficients:

Check that the determinant of u is constant and check the required matrix equation to reasonable precision:

The matrix can have symbolic coefficients:

Check the matrix equation:

Check that u is unimodular; in this case, it is a constant with respect to the polynomial variable x:

Options (3)

Modulus (1)

PolynomialHermiteDecomposition can work modulo a prime:

Check that the determinant of u is constant and check the required matrix equation:

Method (2)

In addition to the default MethodAutomatic, one can specify Method"Direct" to use dedicated univariate polynomial algebra code:

Check the result:

Instead set Method  "GroebnerBasis" (this uses a computation of a module Gröbner basis):

Check the result:

This gives the same result as:

Use different methods with a prime modulus:

Applications (2)

Polynomial Equations (1)

Create an underdetermined system using a 6×8 matrix of random quartic polynomials:

A function to find polynomial solutions to linear systems with polynomial coefficients:

Solve this system:

Check the solution:

One can get a solution faster using LinearSolve:

But several components are rational functions rather than polynomials:

Greatest Common Left Divisor (GCLD) (1)

One can use PolynomialHermiteDecomposition to compute left-extended GCDs of two polynomial matrices.

Construct a pair of matrices with a known nontrivial left common divisor:

Join these transposed and compute the Hermite decomposition:

The GCD matrix is obtained from h:

Create a solver over the univariate polynomial ring:

Use it to recover the GCD cofactors:

Check these:

While a matrix GCD is not unique, any one is related to another by a unimodular transformation.

Construct the unimodular matrix transforming gcd to the common multiplier m3:

Check that is unimodular and transforms gcd to m3:

Properties & Relations (3)

Compute the Hermite normal form of a matrix:

The Hermite normal form can also be obtained from the second matrix returned by PolynomialHermiteDecomposition:

The Hermite form of a matrix is unique only up to constant multiples of the rows:

Only consider second element of second rows to avoid a division by zero:

Create a pair of polynomials with a known common divisor (which is the GCD with high probability):

Compute the extended GCD of this pair:

Compute the Hermite decomposition:

The first row of h will recover the GCD up to a unit factor:

The first row of u will recover the extended GCD multipliers up to a unit factor:

PolynomialHermiteDecomposition works over the Euclidean ring of univariate polynomials:

The entries above any pivot are always lower in degree than that pivot:

The determinant of u must be a nonzero number, as these are exactly the invertible polynomials:

In contrast, HermiteDecomposition works over the Euclidean ring of the integers:

Now the entries above any pivot are always smaller in absolute value than that pivot:

The determinant of u2 must be 1 or , as these are the only invertible integers:

Note that integers and polynomials are different as rings, and in particular one does not recover anything resembling the integer Hermite decomposition by making the polynomial variable zero:

Top

More Learning

Tech Support

Wolfram Solutions

Wolfram Solutions For Education

Get Started

Grow Your Skills

Work with Us

Educational Programs for Adults

Educational Programs for Youth

Read

PolynomialHermiteDecomposition

Details

Examples

Basic Examples (2)

Scope (4)