PrimeOmega

PrimeOmega[n]

n における重複を数えた素因数 の個数を与える．

詳細とオプション

  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • PrimeOmegaは整数の素因数の数を重複も含めて与える．
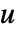  • が標準次数の単数で 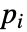が標準次数の素数である数 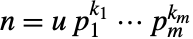について，PrimeOmega[n]は k1+⋯+kmを返す．
  • GaussianIntegers->Trueのとき，PrimeOmegaはガウスの素因数の数を与える．
  • PrimeOmega[m+In]は自動的にガウス整数上で動作する．

例題

すべて開くすべて閉じる

例  (2)

30におけるPrimeOmegaを計算する：

最初の100の数についてPrimeOmega数列をプロットする：

スコープ  (8)

数値評価  (4)

PrimeOmegaは整数に使うことができる：

ガウス整数：

大きい整数について計算する：

PrimeOmegaはリストに縫い込まれる：

記号演算  (4)

TraditionalFormによる表示：

式を削減する：

方程式を解く：

PrimeOmega数列を識別する：

オプション  (1)

GaussianIntegers  (1)

PrimeOmegaを整数上で計算する：

ガウス整数：

アプリケーション  (6)

基本的なアプリケーション  (2)

100までの整数についてのPrimeOmegaの値の表：

PrimeOmegaの値のヒストグラム：

整数論  (4)

PrimeOmegaを使って素数について調べる：

PrimeOmegaを使ってLiouvilleLambdaを計算する：

以下と比較する：

整数引数の異なる範囲でPrimeOmegaの値の平均をプロットする：

PrimeOmega数列についてのフーリエ統計：

特性と関係  (5)

FactorIntegerを使って重複を数えた素因数の数を求める：

PrimeOmegaは完全な加法関数である：

PrimeOmegaは素数ベキの指数を与える：

引数が平方因子を含まない場合，PrimeOmegaおよびPrimeNuは等しい：

PrimeOmegaは常にPrimeNu以上である：

考えられる問題  (1)

PrimeOmegaは0では定義されない：

おもしろい例題  (2)

PrimeOmegaのフーリエ変換の引数をプロットする：

PrimeOmegaのウラム(Ulam)螺線をプロットする：

Wolfram Research (2008), PrimeOmega, Wolfram言語関数， https://reference.wolfram.com/language/ref/PrimeOmega.html.

テキスト

Wolfram Research (2008), PrimeOmega, Wolfram言語関数， https://reference.wolfram.com/language/ref/PrimeOmega.html.

CMS

Wolfram Language. 2008. "PrimeOmega." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PrimeOmega.html.

APA

Wolfram Language. (2008). PrimeOmega. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PrimeOmega.html

BibTeX

@misc{reference.wolfram_2024_primeomega, author="Wolfram Research", title="{PrimeOmega}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/PrimeOmega.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_primeomega, organization={Wolfram Research}, title={PrimeOmega}, year={2008}, url={https://reference.wolfram.com/language/ref/PrimeOmega.html}, note=[Accessed: 21-December-2024 ]}