WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

PrimePi[x]

x 以下の素数 TemplateBox[{x}, PrimePi]の数を与える．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
数値評価  
記号演算  
オプション  
Method  
ProgressReporting  
アプリケーション  
基本的なアプリケーション  
近似  
整数論  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
テクニカルノート
関連するガイド
関連リンク
履歴
引用書式

PrimePi

PrimePi[x]

x 以下の素数 TemplateBox[{x}, PrimePi]の数を与える．

詳細とオプション

  • PrimePiは素数計数関数としても知られている．
  • 記号操作・数値操作の両方に適した数学関数である．
  • TemplateBox[{x}, PrimePi]は x 以下の素数を数える．
  • TemplateBox[{x}, PrimePi]は 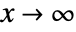のとき漸近展開 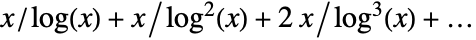を持つ．
  • 次は，使用可能なオプションである．
  • Method Automatic使用するメソッド
    ProgressReporting $ProgressReporting計算の進捗状況を報告するかどうか
  • 次は，Methodの可能な設定である．
  • "DelegliseRivat"Deléglise–Rivatアルゴリズムを使う
    "Legendre"ルジャンドル(Legendre)の公式を使う
    "Lehmer"レーマー(Lehmer)の公式を使う
    "LMO"Lagarias–Miller–Odlyzkoのアルゴリズムを使う
    "Meissel"Meisselの公式を使う
    "Sieve"エラストテネス(Erastosthenes)の篩を使う

例題

すべて開く すべて閉じる

例  (3)

15までの素数を計算する：

Wolfram Language code: PrimePi[15]

素数の計数関数をプロットする：

Wolfram Language code: Plot[PrimePi[x], {x, 0, 50}]

InfinityにおけるPrimePiの最高次の漸近を求める：

Wolfram Language code: Asymptotic[PrimePi[x], x -> Infinity]

スコープ  (10)

数値評価  (5)

PrimePiは整数に使うことができる：

Wolfram Language code: PrimePi[100]

有理数に使う：

Wolfram Language code: PrimePi[7 / 2]

実数に使う：

Wolfram Language code: PrimePi[15.25]

PrimePiは大きい数に使うことができる：

Wolfram Language code: PrimePi[10 ^ 15]

PrimePiはリストに縫い込まれる：

Wolfram Language code: PrimePi[{3, 5, 17, 25}]

記号演算  (5)

PrimePiの従来の数学表記：

Wolfram Language code: PrimePi[x]//TraditionalForm

PrimePiを含む方程式の解の例を求める：

Wolfram Language code: FindInstance[PrimePi[n] == 7, n, Integers]

積分を評価する：

Wolfram Language code: Integrate[PrimePi[x ^ 2], {x, 0, 10}]

PrimePi関数を認識する：

Wolfram Language code: FindSequenceFunction[{0, 1, 2, 2, 3, 3, 4, 4, 4, 4}, n]

漸近関係を求める：

Wolfram Language code: Asymptotic[PrimePi[x], x -> Infinity]

漸近関係を確かめる：

Wolfram Language code: AsymptoticEquivalent[PrimePi[x], LogIntegral[x], x -> Infinity]

オプション  (6)

Method  (5)

素数の計数に使うためにルジャンドル(Legendre)法を指定する[MathWorld]：

Wolfram Language code: PrimePi[10 ^ 6, Method -> "Legendre"]

計算時間を比較する：

Wolfram Language code: BarChart[Table[{First[AbsoluteTiming[PrimePi[10 ^ n]]], First[AbsoluteTiming[PrimePi[10 ^ n, Method -> "Legendre"]]]}, {n, 7, 11, .5}], ChartLegends -> {"Automatic", "Legendre"}]

素数の計数に使うためにレーマー(Lehmer)法を指定する[MathWorld]：

Wolfram Language code: PrimePi[10 ^ 6, Method -> "Lehmer"]

計算時間を比較する：

Wolfram Language code: BarChart[Table[{First[AbsoluteTiming[PrimePi[10 ^ n]]], First[AbsoluteTiming[PrimePi[10 ^ n, Method -> "Lehmer"]]]}, {n, 7, 11, .5}], ChartLegends -> {"Automatic", "Lehmer"}]

素数の計数に使うためにDeléglise–Rivat法を指定する：

Wolfram Language code: PrimePi[10 ^ 6, Method -> "DelegliseRivat"]

計算時間を比較する：

Wolfram Language code: BarChart[Table[{First[AbsoluteTiming[PrimePi[10 ^ n]]], First[AbsoluteTiming[PrimePi[10 ^ n, Method -> "DelegliseRivat"]]]}, {n, 7, 11, .5}], ChartLegends -> {"Automatic", "Deleglise-Rivat"}]

素数の計数に使うためにMeissel法を指定する[MathWorld]：

Wolfram Language code: PrimePi[10 ^ 6, Method -> "Meissel"]

計算時間を比較する：

Wolfram Language code: BarChart[Table[{First[AbsoluteTiming[PrimePi[10 ^ n]]], First[AbsoluteTiming[PrimePi[10 ^ n, Method -> "Meissel"]]]}, {n, 7, 11, .5}], ChartLegends -> {"Automatic", "Meissel"}]

素数の計数に使うためにLagarias–Miller–Odlyzko (LMO) を指定する：

Wolfram Language code: PrimePi[10 ^ 6, Method -> "LMO"]

計算時間を比較する：

Wolfram Language code: BarChart[Table[{First[AbsoluteTiming[PrimePi[10 ^ n]]], First[AbsoluteTiming[PrimePi[10 ^ n, Method -> "LMO"]]]}, {n, 7, 11, .5}], ChartLegends -> {"Automatic", "Lagarias-Miller-Odlyzko"}]

ProgressReporting  (1)

デフォルトで，PrimePiは進捗状況を報告しない：

Wolfram Language code: PrimePi[10 ^ 17 + 1]

ProgressReporting->Trueと設定すると，PrimePiは計算の進捗状況を表示するようになる：

Wolfram Language code: PrimePi[10 ^ 17 + 1, ProgressReporting -> True]

アプリケーション  (22)

基本的なアプリケーション  (7)

PrimePi関数を可視化する：

Wolfram Language code: Grid[Prepend[Table[{"10" ^ n, PrimePi[10 ^ n]}, {n, 1, 10}], {"x", "π(x)"}], ...]

PrimePiの螺線：

Wolfram Language code: ListPolarPlot[Table[{Mod[π / 2 - n 4π / 50, 2π], PrimePi[n]}, {n, 50}], ...]

素数の六角螺線：

Wolfram Language code: hexagonalSpiral[n_] := {Re[#], Im[#]}& /@ Fold[Join[#1, Last[#1] + Exp[I Pi / 3] ^ #2Range[#2 / 2]]&, {0}, Range[n]]
Wolfram Language code: spiral = hexagonalSpiral[25];
Wolfram Language code: primes = spiral[[Prime[Range[PrimePi[Length[spiral]]]]]];
Wolfram Language code: ListPlot[spiral, ...]

PrimePi関数のContourPlot：

Wolfram Language code: ListContourPlot[Table[{x = n, y = PrimePi[n]}, {n, 1, 25}]]

RiemannR関数とPrimePi関数の差をプロットする：

Wolfram Language code: r = 0;c = -1;ListPolarPlot[{Table[{i * Pi / 8, x = RiemannR[i] - PrimePi[i];If[x > c, c = x;r = r + 1];PrimePi[i] * r / i}, {i, 1000}]}, Rule[...]]

100以下のすべての素数を求める：

Wolfram Language code: Prime[Range[PrimePi[100]]]

ある区間の素数の数を数える：

Wolfram Language code: primecount[{x_, y_}] := PrimePi[y + 1] - PrimePi[x - 1]
Wolfram Language code: primecount[{5, 15}]

近似  (7)

PrimePiの近似：

Wolfram Language code: PrimePi[5000]
Wolfram Language code: 5000 / Log[5000.]
Wolfram Language code: LogIntegral[5000.]
Wolfram Language code: RiemannR[5000.]

PrimePiを推定値と比較してプロットする：

Wolfram Language code: Plot[{PrimePi[x], x / Log[x], LogIntegral[x], RiemannR[x]}, {x, 1.5, 100}, Rule[...]]

3より大きい について，TemplateBox[{x}, PrimePi]はが下界で が上界である：

Wolfram Language code: Plot[{x / Log[x], PrimePi[x], x / (Log[x] - 1.112)}, {x, 3, 100}, Rule[...]]

は，について，TemplateBox[{x}, PrimePi]の以内にある：

Wolfram Language code: Plot[{(x/HarmonicNumber[x] - 3 / 2), PrimePi[x]}, {x, 50, 200}, Rule[...]]

リーマン(Riemann)予想が正しければ，について TemplateBox[{{TemplateBox[{x}, PrimePi], -, TemplateBox[{x}, LogIntegral]}}, Abs]<(sqrt(x) log(x))/(8 pi)である：

Wolfram Language code: Plot[{Abs[PrimePi[x] - LogIntegral[x]], Sqrt[x]Log[x] / (8 * Pi)}, {x, 2657, 3000}, PlotLegends -> "Expressions"]

EulerPhiを使って素数を数える：

Wolfram Language code: primecount[x_] := Underoverscript[∑, k = 2, ⌊x⌋]⌊(EulerPhi[k]/k - 1)⌋
Wolfram Language code: Table[primecount[n], {n, 0, 10}]
Wolfram Language code: Table[PrimePi[n], {n, 0, 10}]

Hardy–Wrightの式に基づいてPrimePiを計算する：

Wolfram Language code: primecount[x_] := Sum[Mod[(j - 2)!, j], {j, 4, x}]
Wolfram Language code: Table[primecount[n], {n, 5, 10}]
Wolfram Language code: Table[PrimePi[n], {n, 5, 10}]

Accumulateを使ってPrimePiを計算する：

Wolfram Language code: Accumulate[Table[Boole[PrimeQ[n]], {n, 1, 10}]]
Wolfram Language code: Table[PrimePi[n], {n, 1, 10}]

整数論  (8)

までの双子素数（の形の素数ペア）を求める：

Wolfram Language code: TwinPrimes[n_] := Pick[#, PrimeQ[# + 2]]&[Prime[Range[PrimePi[n]]]]
Wolfram Language code: TwinPrimes[100]
Wolfram Language code: TwinPrimePi[n_] := Length[Pick[#, PrimeQ[# + 2]]]&[Prime[Range[PrimePi[n]]]]

双子素数とPrimePiの列をプロットする：

Wolfram Language code: ListStepPlot[{Table[TwinPrimePi[n], {n, 1, 100}], Table[PrimePi[n], {n, 1, 100}]}]

番目のラマヌジャン素数は，すべての について である最小の数 である：

Wolfram Language code: list = Table[PrimePi[n] - PrimePi[n / 2], {n, 10 ^ 4}];
Wolfram Language code: ramanujanPrime = 1 + Last[Position[list, #]][[1]]& /@ Range[0, 50];
Wolfram Language code: ramanujanPrimePi[n_] := Count[ramanujanPrime, _ ? (# ≤ n&)]

ラマヌジャン素数の列をプロットする：

Wolfram Language code: Plot[ramanujanPrimePi[n], {n, 0, 100}]

ラマヌジャン素数とPrimePiの数を比べる：

Wolfram Language code: Plot[{ramanujanPrimePi[n], PrimePi[n]}, {n, 0, 100}]

番目の素数までの素数積（階乗に似た，連続する素数の乗算）を計算する：

Wolfram Language code: primorial[0] := 1 primorial[1] := 2 primorial[n_] := Times@@Prime@Range[n];
Wolfram Language code: primorial[5]

までの素数積と階乗を比較する：

Wolfram Language code: DiscretePlot[{Log[n!], Log[Times@@Prime[Range[PrimePi[n]]]]}, {n, 1, 50}]

までの素数積と階乗の差をプロットする：

Wolfram Language code: ListLinePlot[If[True, Differences, Identity][Table[Log[(n!/Times@@Prime[Range[PrimePi[n]]])], {n, 1, 100, 1}]], Filling -> Axis]

チェビシェフ(Chebyshev)のシータ関数をプロットする：

Wolfram Language code: chebyshevTheta[n_] := Log[primorial[PrimePi[n]]];
Wolfram Language code: Plot[chebyshevTheta[n], {n, 1, 100}]
Wolfram Language code: DiscretePlot[{chebyshevTheta[n], PrimePi[n]}, {n, 1, 100}]

までの素数ベキを計算する：

Wolfram Language code: primePowers[n_] := Union@@Table[Prime[Range[PrimePi[n ^ (1 / x)]]] ^ x, {x, Log2[n]}]
Wolfram Language code: primePowers[10]
Wolfram Language code: PrimePowerQ[%]

までのすべての素数ベキを数える：

Wolfram Language code: primePowerPi[n_] := PrimePi[n] + Sum[Floor@Log[Prime[k], n] - 1, {k, PrimePi[Sqrt[n]//Floor]}]
Wolfram Language code: primePowerPi[10]

素数ベキの数をグラフにする：

Wolfram Language code: DiscretePlot[primePowerPi[n], {n, 1, 100}]

素数ベキの数をPrimePiと比較する：

Wolfram Language code: DiscretePlot[{primePowerPi[n], PrimePi[n]}, {n, 1, 100}]

について であるとするHardy–Littlewoodの第2の予想を可視化する：

Wolfram Language code: ArrayPlot[((Outer[Plus, #, #]&)[PrimePi[Range[2, 20]]] - Outer[PrimePi[+##1]&, #, #]&)[Range[2, 20]], Rule[...]]

であるなら は2より大きい連続する素数であり，と の間に少なくとも4つの素数があるとするブロカール(Brocard)の予想をプロットする：

Wolfram Language code: ListStepPlot[-Subtract@@@Partition[PrimePi[Prime[Range[100]] ^ 2], 2, 1], Rule[...]]

ゴールドバッハ(Goldbach)の分割，つまり となるような素数(, )のペアを求める：

Wolfram Language code: goldbachPartitions[n_] := IntegerPartitions[2n, {2}, Prime[Range[PrimePi[2n]]]]
Wolfram Language code: goldbachPartitions[50]

ゴールドバッハの予想をグラフにする：

Wolfram Language code: ListPlot[Transpose[{Range[4, 1000, 2], Length /@ Table[IntegerPartitions[i, 2, Table[Prime[n], {n, PrimePi[i]}]], {i, 4, 1000, 2}]}], Rule[...]]

TemplateBox[{x}, PrimePi]=TemplateBox[{x}, EulerPhi]のたった8つの解：

Wolfram Language code: Cases[Range[100], n_ /; PrimePi[n] == EulerPhi[n]]
Wolfram Language code: DiscretePlot[{PrimePi[n], EulerPhi[n]}, {n, 1, 22}, Rule[...]]

特性と関係  (5)

PrimePiの最大定義域：

Wolfram Language code: FunctionDomain[PrimePi[x], x, Complexes]

PrimePiは のときと漸近的に等しい：

Wolfram Language code: AsymptoticEquivalent[PrimePi[x], x / Log[x], x -> Infinity]

LogIntegralとも漸近的に等しい：

Wolfram Language code: AsymptoticEquivalent[PrimePi[x], LogIntegral[x], x -> Infinity]

PrimePiはPrimeの逆関数である：

Wolfram Language code: PrimePi[Prime[100]]

PrimeQを使って素数を数える：

Wolfram Language code: Count[Table[PrimeQ[n], {n, 1, 1000}], True]
Wolfram Language code: PrimePi[1000]

数学関数の実体：

Wolfram Language code: Entity["MathematicalFunction", "PrimePi"]

PrimePiの積分表現：

Wolfram Language code: Entity["MathematicalFunction", "PrimePi"]["IntegralRepresentations"]

考えられる問題  (1)

評価時間は指数的に増大する：

Wolfram Language code: ListLinePlot[Table[First[AbsoluteTiming[PrimePi[10 ^ n]]], {n, 14, 19, .5}], ...]

おもしろい例題  (3)

PrimePiの値の差に基づいて彩色されたウラム(Ulam)の螺線：

Wolfram Language code: ulam[n_] := Partition[Permute[Range[n ^ 2], Accumulate[Take[Flatten[{{n ^ 2 + 1} / 2, Table [(-1) ^ j i, {j, n}, {i, {-1, n}}, {j}]}], n ^ 2]]], n]
Wolfram Language code: ArrayPlot[PrimePi[ulam[101] + 10] - PrimePi[ulam[101]], Rule[...]]

PrimePi関数に基づいた経路を生成する：

Wolfram Language code: Graphics[Line[AnglePath[Table[PrimePi[n], {n, 1, 1000}]], Rule[...]]]

より小さい素数によって生成された有向グラフを使って多面体を構築する：

Wolfram Language code: vertexcoords[p_] := GraphEmbedding[Graph3D[Flatten[Table[i -> Mod[i * q, p], {i, 1, p - 1}, {q, Prime[Range[PrimePi[p] - 1]]}]]]]
Wolfram Language code: Table[ConvexHullMesh[vertexcoords[p], Rule[...]], {p, Prime[Range[4, 7]]}]
Wolfram Research (1991), PrimePi, Wolfram言語関数， https://reference.wolfram.com/language/ref/PrimePi.html （2021年に更新）.

テキスト

Wolfram Research (1991), PrimePi, Wolfram言語関数， https://reference.wolfram.com/language/ref/PrimePi.html （2021年に更新）.

CMS

Wolfram Language. 1991. "PrimePi." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/PrimePi.html.

APA

Wolfram Language. (1991). PrimePi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PrimePi.html

BibTeX

@misc{reference.wolfram_2026_primepi, author="Wolfram Research", title="{PrimePi}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/PrimePi.html}", note=[Accessed: 03-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_primepi, organization={Wolfram Research}, title={PrimePi}, year={2021}, url={https://reference.wolfram.com/language/ref/PrimePi.html}, note=[Accessed: 03-November-2026]}