

ZetaZero
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
- For positive k, ZetaZero[k] represents the zero of
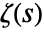 on the critical line
on the critical line 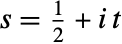 that has the k
that has the k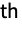 smallest positive imaginary part.
smallest positive imaginary part. - For negative k, ZetaZero[k] represents zeros with progressively larger negative imaginary parts.
- N[ZetaZero[k]] gives a numerical approximation to the specified zero.
- ZetaZero can be evaluated to arbitrary numerical precision.
- ZetaZero automatically threads over lists.
Examples
open all close allBasic Examples (3)
Scope (8)
Numerical Evaluation (3)
Specific Values (3)
Visualization (2)
Generalizations & Extensions (1)
Negative order is interpreted as a reflected root of the Zeta function:
Applications (5)
Plot distances between successive zeros:
Compute Gram points:
Show good Gram points, where RiemannSiegelZ changes sign for consecutive points:
First occurrence of Lehmer's phenomenon:
Plot an approximation of the number of primes and prime powers using MangoldtLambda and ZetaZero:
Properties & Relations (1)
Possible Issues (1)
ZetaZero[0] is not defined:
See Also
Tech Notes
History
Text
Wolfram Research (2007), ZetaZero, Wolfram Language function, https://reference.wolfram.com/language/ref/ZetaZero.html.
CMS
Wolfram Language. 2007. "ZetaZero." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ZetaZero.html.
APA
Wolfram Language. (2007). ZetaZero. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ZetaZero.html
BibTeX
@misc{reference.wolfram_2025_zetazero, author="Wolfram Research", title="{ZetaZero}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/ZetaZero.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_zetazero, organization={Wolfram Research}, title={ZetaZero}, year={2007}, url={https://reference.wolfram.com/language/ref/ZetaZero.html}, note=[Accessed: 17-January-2026]}