Prism

Prism[{p1,…,p6}]

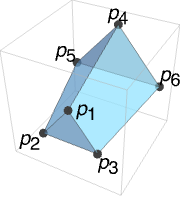
三角形{p1,p2,p3}と{p4,p5,p6}を繋げる塗り潰された角柱を表す．

詳細とオプション

  • Prismは，幾何領域としてあるいはグラフィックスプリミティブとして使うことができる．
  • Prismは，{p1,p3,p6,p4}，{p2,p1,p4,p5}，{p6,p3,p2,p5}，{p1,p2,p3}，{p4,p6,p5}の多角形面で与えられる塗り潰された多面体を表す．
  • CanonicalizePolyhedronを使って角柱を明示的なPolyhedronオブジェクトに変換できる．
  • Prismは，Graphics3Dで使える．
  • グラフィックスでは，点 pi は，ScaledおよびDynamicの式になり得る．
  • グラフィックスの描画は，FaceForm，EdgeForm，Opacity，Texture，色等の指示子に影響される．
  • グラフィックスで使える設定とオプション
  • VertexColorsAutomatic補間される頂点の色
    VertexNormalsAutomatic陰影のための有効な頂点の法線
    VertexTextureCoordinatesNoneテクスチャのための座標

例題

すべて開くすべて閉じる

例  (3)

角柱：

スタイルの付いた角柱：

体積と重心：

スコープ  (18)

グラフィックス  (8)

指定  (2)

単一の角柱：

複数の角柱：

スタイリング  (3)

FaceFormおよびEdgeFormを使って面と辺のスタイルを指定することができる：

Textureを面に適用する：

VertexColorsを頂点に割り当てる：

座標  (3)

プロット範囲との割合で座標を指定する：

一般的な座標からスケールされたオフセットを指定する：

点はDynamicでもよい：

領域  (10)

埋込み次元は，角柱がある空間の次元である：

幾何次元は形それ自体の次元である：

帰属判定：

帰属条件を得る：

体積：

重心：

点からの距離：

角柱の等距離等高線：

点からの符号付き距離：

領域内の最近点：

包み込んでいる球に最近点：

角柱は有界である：

その範囲を求める：

角柱の領域上で積分する：

角柱の領域上で最適化する：

角柱の領域内で方程式を解く：

特性と関係  (2)

角柱は，3つの四面体の和集合として表すことができる：

四面体の頂点の点指標リスト：

ImplicitRegionは，任意のPrismの領域を表すことができる：

おもしろい例題  (1)

軸の周りで角柱を素早く動かす：

Wolfram Research (2014), Prism, Wolfram言語関数， https://reference.wolfram.com/language/ref/Prism.html （2019年に更新）.

テキスト

Wolfram Research (2014), Prism, Wolfram言語関数， https://reference.wolfram.com/language/ref/Prism.html （2019年に更新）.

CMS

Wolfram Language. 2014. "Prism." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Prism.html.

APA

Wolfram Language. (2014). Prism. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Prism.html

BibTeX

@misc{reference.wolfram_2024_prism, author="Wolfram Research", title="{Prism}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Prism.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_prism, organization={Wolfram Research}, title={Prism}, year={2019}, url={https://reference.wolfram.com/language/ref/Prism.html}, note=[Accessed: 21-November-2024 ]}