ProbitModelFit

ProbitModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]

构建形为 的二项概率回归模型，拟合每个 xi 的 yi.

ProbitModelFit[data,{f1,f2,…},{x1,x2,…}]

构建一个二项概率回归模型，形式为 ，其中 fi 与变量 xk 相关.

ProbitModelFit[{m,v}]

从设计矩阵 m 和响应向量 v 构建一个二项概率回归模型.

更多信息和选项

  • ProbitModelFit 试图同时使用 probit 函数 (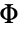) 的反函数和基函数的线性组合对数据建模.
  • LogitModelFit 通常用在分类中，对概率值建模.
  • ProbitModelFit 给出形为 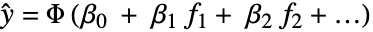的通用线性模型，假定原始的 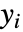是概率为 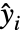的伯努利试验的独立实现.
  • 函数 是标准 NormalDistribution 的 CDF.
  • ProbitModelFit 返回一个符号 FittedModel 对象，表示构建的概率模型. 模型的属性和诊断可以从 model["property"] 得到.
  • ProbitModelFit 在特定点 x1，…… 的最佳拟合函数的值可以从 model[x1,…] 求出.
  • data 的可能的形式为：
  • {y1,y2,…}与形式 {{1,y1},{2,y2},…} 等价
    {{x11,x12,…,y1},…}独立值 xij 列表和响应 yi
    {{x11,x12,…}y1,…}输入值和响应构成的规则列表
    {{x11,x12,…},…}{y1,y2,…}输入值列表和响应构成的规则
    {{x11,…,y1,…},…}n拟合矩阵的第 n 列
  • 在多元数据的情况下，如 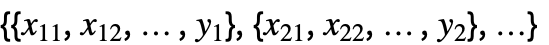{{x_(11),x_(12),... ,y_(1)},{x_(21),x_(22),... ,y_(2)},...}，坐标 xi1、xi2、… 的数量应等于变量 xi 的数量.
  • yi 的概率位于 0 和 1 之间.
  • 另外，可用设计矩阵指定 data，不指定函数和变量：
  • {m,v}设计矩阵 m 和响应向量 v
  • 在 ProbitModelFit[{m,v}] 中，设计矩阵 m 根据在点 {{f1,f2,…},{f1,f2,…},…} 的基函数 fi 形成. 响应向量 v 是响应列表 {y1,y2,…}.
  • 对于一个设计矩阵 m 和响应向量 v，模型是 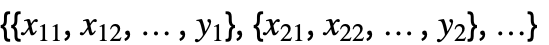，其中 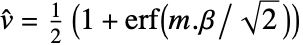是估计参数的向量.
  • 当使用一个设计矩阵，基函数 fi 可以用形式 ProbitModelFit[{m,v},{f1,f2,…}] 指定.
  • ProbitModelFit 等价于 GeneralizedLinearModelFit，其中 ExponentialFamily->"Binomial" 和 LinkFunction->"ProbitLink".
  • ProbitModelFit 采用和 GeneralizedLinearModelFit 相同的选项，除了 ExponentialFamily 和 LinkFunction.

范例

打开所有单元关闭所有单元

基本范例  (1)

定义一个数据集：

拟合一个概率模型：

计算在某个点的模型：

绘制数据点和模型：

范围  (13)

数据  (6)

假设增大的整数独立数值，拟合含有连续概率响应的数据：

这相当于：

按每个预测值的观测次数加权：

这给出相同的最佳拟合函数：

拟合规则列表：

拟合输入值和响应构成的规则：

指定一列数据作为响应：

拟合一个设计矩阵和响应向量给出的模型：

查看函数形式：

拟合涉及 和 的基函数的模型：

得到现有属性列表：

属性  (7)

数据 & 拟合函数  (1)

拟合一个概率模型：

提取原数据：

得到并绘制最佳拟合：

得到纯函数形式的拟合函数：

得到拟合的设计矩阵和响应向量：

残差  (1)

检查拟合的残差：

可视化显示原残差：

在图形中可视化显示 Anscombe 残差和标准化 Pearson 残差：

离差和偏差  (1)

对某些数据拟合一个概率模型：

缺省下估计的离差是 1：

用 Pearson 作为离差估计：

绘制每个点的异常：

分析偏差表：

从表格得到残差异常：

参数估计诊断  (1)

从参数信息中得到一个格式化的表：

提取 -统计值的列：

影响度量  (1)

在对数模型中拟合包含极值的某些数据：

检查 Cook 距离，识别更高的影响点：

检查帽子矩阵的对角元素，估计拟合的数据点的影响：

预测值  (1)

拟合一个概率模型：

绘制于观察值对应的预期值：

拟合优度度量  (1)

得到一个概率模型的拟合优度度量的表格：

计算所有预期变量的子集的拟合优度度量：

通过 AIC 的模型排列：

推广和延伸  (1)

在模型的函数形式上执行其它的数学操作：

符号积分和数值积分：

求出一个预期值，给出模型的一个特定值：

选项  (8)

ConfidenceLevel  (1)

缺省给出 95% 置信区间：

用 99% 的置信区间：

在 FittedModel 中设置级别为 90%：

CovarianceEstimatorFunction  (1)

拟合一个概率模型：

用预期的信息矩阵计算协方差矩阵：

用观察信息矩阵：

DispersionEstimatorFunction  (1)

拟合一个概率模型：

计算协方差矩阵：

计算协方差矩阵，估计 Pearson 的离差：

IncludeConstantBasis  (1)

拟合一个概率模型：

拟合有零常数项的模型：

LinearOffsetFunction  (1)

拟合一个概率模型：

拟合有已知 Sqrt[x] 常数项的模型：

NominalVariables  (1)

拟合数据，将第一个变量视为一个名义变量：

将两个变量视为名义变量：

Weights  (1)

用相等权重拟合一个模型：

对于数据点给出明确的权重：

WorkingPrecision  (1)

用 WorkingPrecision 在参数估计中得到更高的精度：

得到拟合函数：

在拟合后，化简属性计算中的精度：

属性和关系  (4)

ProbitModelFit 中一个缺省的 "Binomial" 模型等价于有 "ProbitLink" GeneralizedLinearModelFit 的模型：

LogitModelFit 是一个从 GeneralizedLinearModelFit 产生的有缺省 "LogitLink" 的一个 "Binomial" 模型：

ProbitModelFit 假设二项分布响应：

NonlinearModelFit 通常假设分布响应：

拟合结果不相同：

ProbitModelFit 将 TimeSeries 的时间戳用作变量：

对时间戳进行缩放，然后重新拟合：

对数值进行拟合：

对于多路径 TemporalData，ProbitModelFit 按路径进行处理：

可能存在的问题  (1)

在 0 到 1 范围外的响应对于概率模型可能没有效果：

Wolfram Research (2008)，ProbitModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ProbitModelFit.html.

文本

Wolfram Research (2008)，ProbitModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ProbitModelFit.html.

CMS

Wolfram 语言. 2008. "ProbitModelFit." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ProbitModelFit.html.

APA

Wolfram 语言. (2008). ProbitModelFit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ProbitModelFit.html 年

BibTeX

@misc{reference.wolfram_2024_probitmodelfit, author="Wolfram Research", title="{ProbitModelFit}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/ProbitModelFit.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_probitmodelfit, organization={Wolfram Research}, title={ProbitModelFit}, year={2008}, url={https://reference.wolfram.com/language/ref/ProbitModelFit.html}, note=[Accessed: 21-November-2024 ]}