RandomSample

RandomSample[{e1,e2,…},n]

gives a pseudorandom sample of n of the ei.

RandomSample[{w1,w2,…}{e1,e2,…},n]

gives a pseudorandom sample of n of the ei chosen using weights wi.

RandomSample[{e1,e2,…}]

gives a pseudorandom permutation of the ei.

Details

  • RandomSample is also known as simple random sampling or sampling without replacement.
  • RandomSample[{e1,e2,…},n] never samples any of the 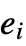e_(i) more than once.
  • RandomSample[{e1,e2,…},n] samples each of the 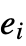e_(i) with equal probability.
  • RandomSample[{e1,e2,…},UpTo[n]] gives a sample of n of the ei, or as many as are available.
  • RandomSample[i;;j;;k,n] may be used to sample the Span from i to j in steps of k.
  • RandomSample gives a different sequence of pseudorandom choices whenever you run the Wolfram Language. You can start with a particular seed using SeedRandom.
  • A Method option to SeedRandom can be given to specify the pseudorandom generator used.

Examples

open allclose all

Basic Examples  (3)

Find a sample in which no elements ever occur more than once:

Generate a random permutation:

Generate a random sample of 6 elements, or as many as there are if fewer:

Scope  (4)

The elements can be any expressions:

With larger weights for later elements, later elements tend to be selected for the sample:

Sample over all numbers between -10 and 10:

Sample over even numbers between -10 and 10:

Guarantee that a set of random integers over a big range has no repetitions:

Applications  (1)

Successively fill in black squares down the page:

Properties & Relations  (3)

Use SeedRandom to get repeatable random values:

Use BlockRandom to block one use of RandomSample from affecting others:

RandomSample of size 1 follows the same distribution as RandomChoice:

Possible Issues  (1)

If the sample size is larger than the population size, an error message is returned:

Wolfram Research (2007), RandomSample, Wolfram Language function, https://reference.wolfram.com/language/ref/RandomSample.html (updated 2015).

Text

Wolfram Research (2007), RandomSample, Wolfram Language function, https://reference.wolfram.com/language/ref/RandomSample.html (updated 2015).

CMS

Wolfram Language. 2007. "RandomSample." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/RandomSample.html.

APA

Wolfram Language. (2007). RandomSample. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RandomSample.html

BibTeX

@misc{reference.wolfram_2024_randomsample, author="Wolfram Research", title="{RandomSample}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/RandomSample.html}", note=[Accessed: 14-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_randomsample, organization={Wolfram Research}, title={RandomSample}, year={2015}, url={https://reference.wolfram.com/language/ref/RandomSample.html}, note=[Accessed: 14-December-2024 ]}