RegionDistance
RegionDistance[reg,p]
gives the minimum distance from the point p to the region reg.
RegionDistance[reg1,reg2]
gives the minimum distance between points in the regions reg1 and reg2.
RegionDistance[reg]
gives a RegionDistanceFunction[…] that can be applied repeatedly to different points.
Details and Options
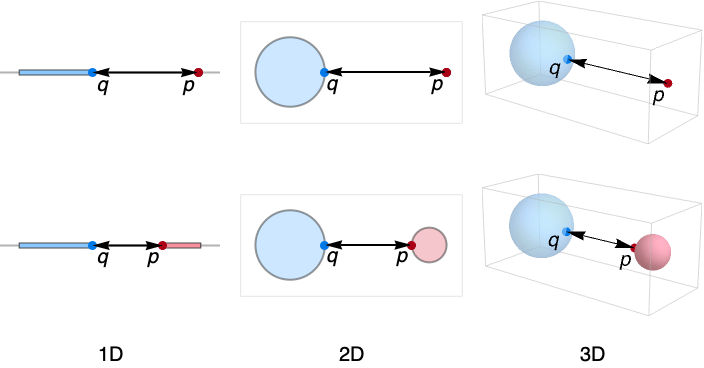
- RegionDistance is also known as point-to-region distance, distance transform, distance field and minimum region distance.
- RegionDistance measures how close two regions are to each other.
- The distance between points q and p is taken to be Norm[p-q].
- RegionDistance[reg,p] is effectively given by MinValue[{Norm[p-q],q∈reg},q].
- RegionDistance[reg1,reg2] is effectively given by MinValue[Norm[p-q],{p∈reg1,q∈reg2}].
- Unless the regions are closed, the nearest distance may not be attained by points in the region but in the closure of the regions.
Examples
open allclose allBasic Examples (2)
Find the distance from a point to the unit disk:
Plot the distance as a function of position:
Find the distance from a point to a MeshRegion:
With one argument, you get a RegionDistanceFunction:
Apply the distance function lists of points to compute many distances:
Scope (15)
Special Regions (9)
Formula Regions (2)
The distance to a disk represented as an ImplicitRegion:
The distance to a disk represented as a ParametricRegion:
Mesh Regions (1)
Derived Regions (3)
The distance to a RegionIntersection:
The distance to a TransformedRegion:
The distance to a RegionBoundary:
Applications (5)
Compute the height of a triangle:
Create a region that is a distance 
from a circle:
Visualize the region and circle:
Compute the dilation of a region:
The directed Hausdorff distance from region 
to 
is defined as 
. Use RegionDistance to compute the directed Hausdorff distance from =Triangle[{{0,0},{2,0},{0,1}}] to ℬ=Triangle[{{0,0},{1,0},{0,3/2}}]:
Find the nearest distance to any point in 
:
As expected, the distance is zero for points in 
that overlap with 
:
Find the directed Hausdorff distance by maximizing over 
:
If 
, you can conclude that 
where 
is the closure of 
and 
. Show that 
for the regions in this example:
The Hausdorff distance between region 
and 
is defined as 
where 
is the directed Hausdorff distance in the previous example. Use RegionDistance to compute the Hausdorff distance between =Triangle[{{0,0},{2,0},{0,1}}] and ℬ=Triangle[{{0,0},{1,0},{0,3/2}}]:
Find the directed Hausdorff distances:
If 
, you can conclude that 
and 
, as in the previous example. Show that 
and 
for the regions in this example:
Properties & Relations (4)
A point is a RegionMember if the distance to the region is 0:
RegionDistance is the MinValue of the distance to any point in the region:
RegionNearest gives a point that is of minimal distance from the input:
For a point outside the region, RegionDistance and SignedRegionDistance are the same:
Text
Wolfram Research (2014), RegionDistance, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionDistance.html (updated 2023).
CMS
Wolfram Language. 2014. "RegionDistance." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/RegionDistance.html.
APA
Wolfram Language. (2014). RegionDistance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionDistance.html