RegionHausdorffDistance

RegionHausdorffDistance[reg1,reg2]

给出区域 reg1 和 reg2 之间的 Hausdorff 距离.

更多信息和选项

  • RegionHausdorffDistance 亦称为 Hausdorff 度量和 Pompeiu–Hausdorff 距离.
  • Hausdorff 距离量度两个区域之间的差别有多大.
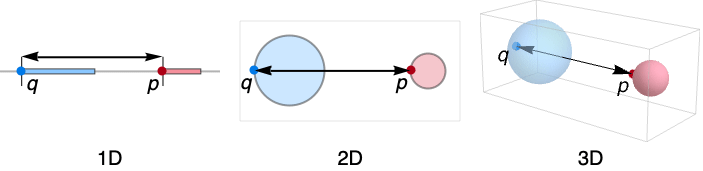
  • RegionHausdorffDistance 是从一个区域中的点到另一个区域中最近点的所有距离中的最大值.
  • 点 p 和 q 之间的距离为 Norm[p-q].
  • 实际上 RegionHausdorffDistance 由 MaxValue[MinValue[Norm[p-q],q∈reg2],p∈reg1] 和 MaxValue[MinValue[Norm[p-q],q∈reg1],p∈reg2] 的最大值给出.
  • 除非区域是闭合的，否则 Hausdorff 距离可能不是通过区域中的点而是通过区域的闭包获得的.
  • 如果 reg1⊆RegionDilation[reg2,ϵ] 和 reg2⊆RegionDilation[reg1,ϵ]，则两个区域 reg1 和 reg2 之间的 Hausdorff 距离为 ϵ.

范例

打开所有单元关闭所有单元

基本范例  (4)

求两个圆盘之间的 Hausdorff 距离：

显示圆盘：

求单位圆盘与正多边形之间的 Hausdorff 距离：

显示区域：

绘制随着边数的增加 Hausdorff 距离的变化：

求出两簇点之间的 Hausdorff 距离：

求 MeshRegion 与其凸包之间的 Hausdorff 距离：

显示凸包：

范围  (9)

特殊区域  (8)

点：

RegionHausdorffDistance 接受坐标列表：

线：

多边形：

单纯形：

盒子：

球：

球面：

n 中的区域：

网格区域  (1)

两个一维网格之间的 Hausdorff 距离：

2D：

3D：

选项  (2)

WorkingPrecision  (2)

RegionHausdorffDistance 将尝试使用与输入相同的精度来计算距离：

用机器算术计算距离：

某些情况下，无法计算出精确的答案：

用 30 位精度求 RegionHausdorffDistance：

应用  (1)

区域构建  (1)

根据随机点样本重建网格：

计算实际物体和重建网格之间的 Hausdorff 距离：

绘制 Hausdorff 距离如何随着样本数量的增加而减小：

属性和关系  (4)

两点之间的 Hausdorff 距离等价于 EuclideanDistance：

两个点集之间的 Hausdorff 距离是任意点到另一点集的最大 EuclideanDistance：

区域与一个点之间的 Hausdorff 距离是该点到该区域中任意点的最远距离：

RegionDistance 可用于求点到区域的最近距离：

Wolfram Research (2023)，RegionHausdorffDistance，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html.

文本

Wolfram Research (2023)，RegionHausdorffDistance，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html.

CMS

Wolfram 语言. 2023. "RegionHausdorffDistance." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html.

APA

Wolfram 语言. (2023). RegionHausdorffDistance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html 年

BibTeX

@misc{reference.wolfram_2025_regionhausdorffdistance, author="Wolfram Research", title="{RegionHausdorffDistance}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html}", note=[Accessed: 04-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_regionhausdorffdistance, organization={Wolfram Research}, title={RegionHausdorffDistance}, year={2023}, url={https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html}, note=[Accessed: 04-April-2025 ]}