単位円上に等間隔で置かれた n 個の頂点がある正多角形を与える.
RegularPolygon[r,n]
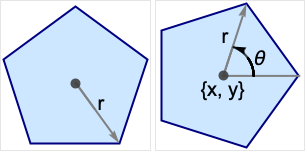
半径 r の正多角形を与える.
RegularPolygon[{r,θ},n]
![]() 軸に対して角 θ から始める.
軸に対して角 θ から始める.
RegularPolygon[{x,y},rspec,n]
多角形の中心を{x,y}にする.


RegularPolygon
単位円上に等間隔で置かれた n 個の頂点がある正多角形を与える.
RegularPolygon[r,n]
半径 r の正多角形を与える.
RegularPolygon[{r,θ},n]
![]() 軸に対して角 θ から始める.
軸に対して角 θ から始める.
RegularPolygon[{x,y},rspec,n]
多角形の中心を{x,y}にする.
詳細とオプション

- RegularPolygonは,幾何学領域およびグラフィックスプリミティブとして使うことができる.
- 角 θ は,正の x 方向から反時計回りにラジアン単位で計測される.
- 整数 n についてのRegularPolygonは,連続する点の間の角度が等しい多角形を表す.
- CanonicalizePolygonを使って正多角形を明示的なPolygonオブジェクトに変換することができる.
- RegularPolygonはGraphicsで使うことができる.
- グラフィックスでは,点{x,y}は,Scaled,Offset,ImageScaled,Dynamicの式でよく,半径 r は,Scaled,ImageScaled,Dynamicでよい.
- グラフィックスの描画は,FaceForm,EdgeForm,色等の指示子の影響を受ける.
例題
すべて開く すべて閉じる例 (3)
スコープ (17)
グラフィックス (7)
アプリケーション (4)
共通の原点を中心にして回転させた三角形のRegionUnionを取り,星の領域を作る:
RegionProductで3Dの押出し形成を作る:
特性と関係 (3)
RegularPolygonは,![]() 個の頂点が単位円上に等間隔で置かれたPolygonのことである:
個の頂点が単位円上に等間隔で置かれたPolygonのことである:
CirclePointsを使って単位円上に等間隔で置かれた点を生成する:
![]() とした単位円上の正多角形の面積は,単位Diskのそれである:
とした単位円上の正多角形の面積は,単位Diskのそれである:
関連項目
CirclePoints Polygon Triangle Rectangle
Function Repository: RegularPolygonAngleRadius PolygonFromBase
関連するガイド
-
▪
- グラフィックスオブジェクト ▪
- 基本的な特殊領域 ▪
- 平面幾何学 ▪
- 総合幾何学 ▪
- 多角形
テキスト
Wolfram Research (2015), RegularPolygon, Wolfram言語関数, https://reference.wolfram.com/language/ref/RegularPolygon.html (2019年に更新).
CMS
Wolfram Language. 2015. "RegularPolygon." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/RegularPolygon.html.
APA
Wolfram Language. (2015). RegularPolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegularPolygon.html
BibTeX
@misc{reference.wolfram_2025_regularpolygon, author="Wolfram Research", title="{RegularPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/RegularPolygon.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_regularpolygon, organization={Wolfram Research}, title={RegularPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/RegularPolygon.html}, note=[Accessed: 05-February-2026]}