RootIntervals

RootIntervals[{poly1,poly2,…}]

gives a list of isolating intervals for the real roots of any of the polyi, together with a list of which polynomials actually have each successive root.

RootIntervals[poly]

gives isolating intervals for real roots of a single polynomial.

RootIntervals[polys,Complexes]

gives bounding rectangles for complex roots.

Details

  • The coefficients of poly must be integers or rationals.
  • An isolating interval for a root 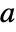of a polynomial poly is an interval where the only root of poly contained in the interval is .
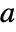  • If a root is real, the isolating interval is an open real interval, or a point. If a root is not real, the isolating interval is an open rectangle, disjoint from the real axis.
  • Multiple roots give multiple entries in the second list generated by RootIntervals.

Examples

open allclose all

Basic Examples  (2)

Get isolating intervals, together with a list of which polynomial has which root:

The isolating intervals are always specified by exact rationals:

Scope  (6)

Isolate the real roots of a polynomial:

Isolate the real roots of a list of polynomials:

Isolate the complex roots of a polynomial:

Isolate the complex roots of a list of polynomials:

Polynomials may have multiple roots; pairs of polynomials may have common roots:

Isolating intervals of rational roots may be single points:

Applications  (1)

Find numeric approximations of real roots of a polynomial:

Find isolating intervals:

Find root approximations:

Reduce uses a similar approach, but factoring the polynomial for Root objects takes time:

Compute approximations of the Root objects:

Properties & Relations  (1)

Find real and complex roots of polynomials:

Isolate the real roots; multiple roots are indicated in the second part of the output:

Use CountRoots to count the real roots; multiple roots are counted with multiplicities:

Use Reduce to find the real roots; multiple roots are given once:

Isolate the complex roots; multiple roots are indicated in the second part of the output:

Use Reduce to find the complex roots; multiple roots are given once:

Use Solve to find the complex roots with multiplicities:

Wolfram Research (2007), RootIntervals, Wolfram Language function, https://reference.wolfram.com/language/ref/RootIntervals.html.

Text

Wolfram Research (2007), RootIntervals, Wolfram Language function, https://reference.wolfram.com/language/ref/RootIntervals.html.

CMS

Wolfram Language. 2007. "RootIntervals." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RootIntervals.html.

APA

Wolfram Language. (2007). RootIntervals. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RootIntervals.html

BibTeX

@misc{reference.wolfram_2024_rootintervals, author="Wolfram Research", title="{RootIntervals}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/RootIntervals.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rootintervals, organization={Wolfram Research}, title={RootIntervals}, year={2007}, url={https://reference.wolfram.com/language/ref/RootIntervals.html}, note=[Accessed: 21-November-2024 ]}