Roots

Roots[lhs==rhs,var]

整方程式の解（根）を表すように方程式を分離する．

詳細とオプション

  • Rootsは，解の検索にFactorやDecomposeを使用する．
  • Nを適用することで解の数値的な値を求めることもできる．
  • Rootsは，以下のオプションを取り込むことができる．
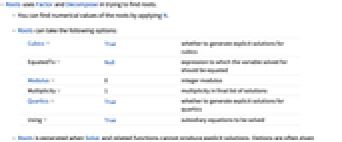
  • Cubics True三次式に明示的な解を作成するかどうか
    EquatedTo Null方程式の変数に等しいとする式
    Modulus 0整数剰余
    Multiplicity 1最終的な解のリストの多重性
    Quartics True四次式に明示的な解を作成するかどうか
    Using True補助方程式の求解
  • Solveやこれに関連した関数が明示的な解を見出せない場合には，Rootsが作成される．このような場合，オプションを与えることが多い．
  • Rootsは，解の多重性が1より大になった場合，複数の同じ方程式を与える．

例題

すべて開くすべて閉じる

例  (1)

一変数整方程式の根を求める：

スコープ  (7)

厳密な数値係数を持つ方程式：

記号係数を持つ方程式：

一般的な五次以上の方程式は根基では解けない：

この九次方程式は因数分解およびその他の分解を使って根基で解ける：

厳密ではない数値係数を持つ方程式：

多重根は対応する回数だけ繰り返される：

7を法とする整数上で根を求める：

オプション  (10)

Cubics  (3)

デフォルトで，Rootsは三次方程式を根基で解くのに一般的な公式を用いる：

Cubics->Falseとすると，Rootsは三次方程式を根基で解くのに一般的な公式を用いない：

この三次方程式を根基で解くのに一般的な公式は必要ない：

EquatedTo  (1)

EquatedToを使って返された方程式の左辺を指定する：

Modulus  (1)

12を法とする整数上で根を求める：

Multiplicity  (1)

Multiplicity->n とすると，各根の多重度が n で乗算される：

Quartics  (3)

デフォルトで，Rootsは四次方程式を根基で解くのに一般的な公式を用いる：

Quartics->Falseとすると，Rootsは四次方程式を解くのに一般的な公式を用いない：

この四次方程式を根基で解くのに一般的な公式は必要ない：

Using  (1)

記号パラメータで満足される方程式を指定する：

特性と関係  (5)

Rootsで返される解は方程式を満足する：

ToRulesを使ってRootsが返す方程式を置換規則に変換する：

SolveはRootsを使って一変数方程式の解を求め，置換規則を返す：

Rootsはすべての複素数解を求める：

Reduceを使って指定した領域上で解を求める：

FindInstanceを使って1つの解を求める：

SolveまたはReduceを使って多変数方程式系の解を求める：

Reduceを使って方程式と不等式の系の解を求める：

NRootsを使って一変数方程式の根の数値近似を求める：

Wolfram Research (1988), Roots, Wolfram言語関数， https://reference.wolfram.com/language/ref/Roots.html.

テキスト

Wolfram Research (1988), Roots, Wolfram言語関数， https://reference.wolfram.com/language/ref/Roots.html.

CMS

Wolfram Language. 1988. "Roots." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Roots.html.

APA

Wolfram Language. (1988). Roots. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Roots.html

BibTeX

@misc{reference.wolfram_2024_roots, author="Wolfram Research", title="{Roots}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Roots.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_roots, organization={Wolfram Research}, title={Roots}, year={1988}, url={https://reference.wolfram.com/language/ref/Roots.html}, note=[Accessed: 14-November-2024 ]}