RowReduce[m]
行列 m に掃出し法を適用した形を示す.


RowReduce
RowReduce[m]
行列 m に掃出し法を適用した形を示す.
詳細とオプション

- RowReduceはガウスの消去を行う.これは複数の行を加算しながら可能な場合にゼロの要素を作成する.最終的な行列は掃き出した行を梯列形式で表す.
- m が非退化正方行列である場合,RowReduce[m]はIdentityMatrix[Length[m]]である. »
- m が
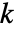 行と
行と 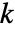 より多くの列を持った非退化矩形行列である場合,RowReduce[m]の先頭の
より多くの列を持った非退化矩形行列である場合,RowReduce[m]の先頭の 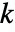 列は単位行列を作る. »
列は単位行列を作る. » - RowReduceは,数値的および記号的行列に対して機能する.
- 次のオプションを与えることができる.
-
Method Automatic 使用するメソッド Modulus 0 使用すべき法とする整数 Tolerance Automatic 使用する数値許容度 ZeroTest Automatic 行列の要素をゼロとみなすかどうかを判別する関数 - RowReduce[m,Modulus->n]は,整数 n を法として有理行列の簡約形を求める.n が0のときは通常の算術演算が用いられる.n が素数ではないときは,計算が失敗する可能性がある. »
- RowReduce[m,ZeroTest->test]は,行列要素がゼロであるかどうかを判定するために test[m[[i,j]]]を評価する.
- Methodオプションの取り得る値は,"CofactorExpansion","DivisionFreeRowReduction","OneStepRowReduction"である.デフォルト設定のAutomaticの場合は,与えられた行列によってこれらのメソッドを使い分ける.
例題
すべて開く すべて閉じるスコープ (13)
オプション (3)
Tolerance (1)
アプリケーション (13)
スパンと線形独立 (5)
方程式の解法と可逆性 (8)
係数行列 ![]() に掃出し法を適用すると恒等行列になるので,この系は一意解を持つ:
に掃出し法を適用すると恒等行列になるので,この系は一意解を持つ:
Solveを使って結果を確かめる:
系 ![]() を解く.ただし,
を解く.ただし, ![]() は行列で
は行列で ![]() はベクトルである.掃出し法を使う:
はベクトルである.掃出し法を使う:
最終列に先行する1があるので,![]() の解はない.Solveを使って確認する:
の解はない.Solveを使って確認する:
0の行があるので,零空間は非空である.拡張行列 ![]() に掃出し法を使う:
に掃出し法を使う:
削減しても恒等行列にはならないので,この行列は可逆ではない:
Inverseを使って結果を確かめる:
削減すると恒等行列になるので,行列式は非零でなくてはならない:
Detを使って結果を確認する:
![]() を削減しても恒等行列にならないなら
を削減しても恒等行列にならないなら ![]() は
は ![]() の固有値である.掃出し法を適用した形における0の行の数よりも大きい多重度を持つ固有値を持つならその行列は不完全行列である.
の固有値である.掃出し法を適用した形における0の行の数よりも大きい多重度を持つ固有値を持つならその行列は不完全行列である.![]() が次の行列
が次の行列 ![]() の固有値であることを示す:
の固有値であることを示す:
Eigenvaluesを使って結果を確認する:
2が2回現れるのに掃出し法を適用した形には0の行が1つしかないので,行列 ![]() は不完全である:
は不完全である:
Eigensystemで結果を確かめると固有ベクトルのリストが0で充填されていることで不完全性が示される:
Inverseを使って結果を確かめる:
特性と関係 (8)
RowReduceは,入力精度にかかわらず,先頭の0を厳密な整数として返す:
RowReduce[m]がIdentityMatrix[Length[m]]のときかつそのときに限って正方行列 m は可逆である:
実際.逆行列は拡張行列の形式を m と単位行列で反転することで求められる:
正方行列では,Det[m]!=0のときかつそのときに限って m に掃出し法を使うと恒等行列になる:
正方行列では,零空間が空のときかつそのときに限って m に掃出し法を使うと恒等行列になる:
正方行列では,LinearSolve[m,b]が一般的な b についての解を持つときかつそのときに限って m に掃出し法を使うと恒等行列になる:
RowReduce[m]の最初の ![]() 列が恒等行列を形成するときかつそのときに限って
列が恒等行列を形成するときかつそのときに限って ![]() である
である ![]() 行列
行列 ![]() の階数は
の階数は ![]() になる:
になる:
MatrixRank[m]はRowReduce[m]における非零の列の数に等しい:
平方行列 m の零空間はRowReduceを使って計算できる:
行の拡張された半分に先頭の1があれば,その半分は零空間にある:
NullSpaceを使って零ベクトルを得る:
関連項目
LinearSolve Inverse NullSpace RangeSpace HermiteDecomposition SmithDecomposition GroebnerBasis
Function Repository: BitStringRowReduce AugmentedMatrix LinearAlgebraMod
テクニカルノート
履歴
1988 で導入 (1.0) | 1996 で更新 (3.0) ▪ 2022 (13.2) ▪ 2024 (14.0)
テキスト
Wolfram Research (1988), RowReduce, Wolfram言語関数, https://reference.wolfram.com/language/ref/RowReduce.html (2024年に更新).
CMS
Wolfram Language. 1988. "RowReduce." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/RowReduce.html.
APA
Wolfram Language. (1988). RowReduce. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RowReduce.html
BibTeX
@misc{reference.wolfram_2025_rowreduce, author="Wolfram Research", title="{RowReduce}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RowReduce.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_rowreduce, organization={Wolfram Research}, title={RowReduce}, year={2024}, url={https://reference.wolfram.com/language/ref/RowReduce.html}, note=[Accessed: 17-February-2026]}