RowReduce[m]
给出矩阵 m 的行约化形式.


RowReduce
RowReduce[m]
给出矩阵 m 的行约化形式.
更多信息和选项

- RowReduce 执行一个高斯消去,将行的倍数累加在一起以尽可能的生成 0 元素. 最后的矩阵为行简阶梯形式.
- 如果 m 是一个非退化方阵,则 RowReduce[m] 是 IdentityMatrix[Length[m]]. »
- 如果 m 是一个具有
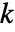 行和超过
行和超过 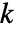 列的充分非退化矩阵,则 RowReduce[m] 的前
列的充分非退化矩阵,则 RowReduce[m] 的前 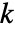 列将形成一个单位矩阵. »
列将形成一个单位矩阵. » - RowReduce 同时适用于数值矩阵和符号矩阵.
- 可以有以下选项:
-
Method Automatic 使用的方法 Modulus 0 使用的整数模 Tolerance Automatic 使用的数值容差 ZeroTest Automatic 测试矩阵元素是否可视为零的函数 - RowReduce[m,Modulus->n] 求有理矩阵对整数 n 取模后的简化形式. 若 n 为零,则使用普通算术运算. 若 n 不是质数,计算可能会失败. »
- RowReduce[m,ZeroTest->test] 计算 test[m[[i,j]]] 来确定矩阵元素是否为零.
- Method 选项可能的设置包括 "CofactorExpansion"、"DivisionFreeRowReduction" 和"OneStepRowReduction". 缺省设置 Automatic 会根据所给的矩阵选择其中的方法.
范例
打开所有单元 关闭所有单元范围 (13)
选项 (3)
Tolerance (1)
应用 (13)
生成空间和线性独立 (5)
求解方程和可逆性 (8)
用 Solve 验证结果:
因为最后一列有一个 1,所以 ![]() 无解;用 Solve 确认:
无解;用 Solve 确认:
用 Inverse 验证结果:
用 Det 确认结果:
如果 ![]() 没有约化为单位矩阵,则
没有约化为单位矩阵,则 ![]() 是
是 ![]() 的特征值. 如果矩阵的特征值的重数大于行约化形式中的零行的数量,则该矩阵是亏损矩阵. 证明
的特征值. 如果矩阵的特征值的重数大于行约化形式中的零行的数量,则该矩阵是亏损矩阵. 证明 ![]() 是以下矩阵
是以下矩阵 ![]() 的特征值:
的特征值:
用 Eigenvalues 确认结果:
矩阵 ![]() 是亏损矩阵,因为 2 出现了两次,但行约化形式只有一行为零:
是亏损矩阵,因为 2 出现了两次,但行约化形式只有一行为零:
用 Eigensystem 确认结果,用零填充特征向量表明了亏损:
估计用 Inverse 验证结果:
属性和关系 (8)
RowReduce 将前导零作为精确整数返回,与输入的精度无关:
当且仅当 RowReduce[m] 等于 IdentityMatrix[Length[m]],方阵 m 可逆:
实际上,可以通过对 m 和单位矩阵形成的增广矩阵求逆得到逆矩阵:
对于方阵,当且仅当 Det[m]!=0,m 才约化为单位矩阵:
对于方阵,当且仅当 LinearSolve[m,b] 对普通的 b 有解,m 才约化为单位矩阵:
一个 ![]() 矩阵
矩阵 ![]() ,如果
,如果 ![]() ,当且仅当 RowReduce[m] 的前
,当且仅当 RowReduce[m] 的前 ![]() 列形成一个单位矩阵的情况下,其秩才为
列形成一个单位矩阵的情况下,其秩才为 ![]() :
:
MatrixRank[m] 等于 RowReduce[m] 中非零行的数量:
可用 RowReduce 计算方阵 m 的零空间:
如果该行在增广的一半中有前导 1,则该行增广的一半在零空间中:
用 NullSpace 获取零向量:
技术笔记
历史
1988年引入 (1.0) | 在以下年份被更新:1996 (3.0) ▪ 2022 (13.2) ▪ 2024 (14.0)
文本
Wolfram Research (1988),RowReduce,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RowReduce.html (更新于 2024 年).
CMS
Wolfram 语言. 1988. "RowReduce." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/RowReduce.html.
APA
Wolfram 语言. (1988). RowReduce. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RowReduce.html 年
BibTeX
@misc{reference.wolfram_2025_rowreduce, author="Wolfram Research", title="{RowReduce}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RowReduce.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_rowreduce, organization={Wolfram Research}, title={RowReduce}, year={2024}, url={https://reference.wolfram.com/language/ref/RowReduce.html}, note=[Accessed: 07-February-2026]}