RussellRaoDissimilarity
给出在布尔向量 u 和 v 之间的 Russell–Rao相异度.
更多信息
- RussellRaoDissimilarity 适用于 True,False 向量和 0、1 向量.
- RussellRaoDissimilarity[u,v] 等价于 (n10+n01+n00)/Length[u],其中
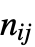 是向量 u 和 v 中对应位置的值分别是 i 和 j 的元素对的数目.
是向量 u 和 v 中对应位置的值分别是 i 和 j 的元素对的数目.
范例
打开所有单元关闭所有单元属性和关系 (4)
Wolfram Research (2007),RussellRaoDissimilarity,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RussellRaoDissimilarity.html.
文本
Wolfram Research (2007),RussellRaoDissimilarity,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RussellRaoDissimilarity.html.
CMS
Wolfram 语言. 2007. "RussellRaoDissimilarity." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RussellRaoDissimilarity.html.
APA
Wolfram 语言. (2007). RussellRaoDissimilarity. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RussellRaoDissimilarity.html 年