Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

RussellRaoDissimilarity

RussellRaoDissimilarity[u,v]

gives the Russell–Rao dissimilarity between Boolean vectors u and v.

Details

RussellRaoDissimilarity works for both True, False vectors and 0, 1 vectors.
RussellRaoDissimilarity[u,v] is equivalent to (n₁₀+n₀₁+n₀₀)/Length[u], where 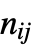is the number of corresponding pairs of elements in u and v respectively equal to i and j.

Examples

open allclose all

Basic Examples (2)

Russell–Rao dissimilarity between two Boolean vectors:

The elements can also be True and False:

Scope (2)

Compute dissimilarity between any 0, 1 vectors of equal length:

Compute dissimilarity between any True, False vectors of equal length:

Properties & Relations (4)

Russell–Rao dissimilarity is bounded by 0 and 1:

RussellRaoDissimilarity is greater than or equal to JaccardDissimilarity:

RussellRaoDissimilarity is greater than or equal to MatchingDissimilarity:

RussellRaoDissimilarity is greater than or equal to DiceDissimilarity:

Top