SchrodingerPDEComponent
SchrodingerPDEComponent[vars,pars]
生成带有模型变量 vars 和模型参数 pars 的薛定谔偏微分方程项.
更多信息



- 生成用于特征系统和瞬态分析的薛定谔方程. 给定变量和参数,返回一个 PDE 算符.
- SchrodingerPDEComponent 是非相对论量子力学中类似于牛顿第二定律的理论,描述了波函数在量子力学中的时间演化.
- SchrodingerPDEComponent 返回用作偏微分方程一部分的微分算子之和:
- SchrodingerPDEComponent 可用于模拟含有自变量
 (单位为
(单位为 ![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/SchrodingerPDEComponent.zh/3.png) )的薛定谔方程,因变量为
)的薛定谔方程,因变量为 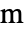 ,单位为
,单位为 ![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]^(-n/2) TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]^(-n/2)](Files/SchrodingerPDEComponent.zh/5.png) ,时间变量为
,时间变量为 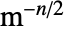 ,单位为
,单位为 ![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/SchrodingerPDEComponent.zh/7.png) .
. - 静态变量 vars 为 vars={Ψ[x1,…,xn],{x1,…,xn}}.
- 时间相关的模型变量 vars 为 vars={Ψ[t,x1,…,xn],t,{x1,…,xn}}.
- SchrodingerPDEComponent 基于动能项和势能项:
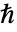 是约化普朗克常数,单位为
是约化普朗克常数,单位为 ![TemplateBox[{InterpretationBox[, 1], {"s", , "J"}, second joules, {"Joules", , "Seconds"}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "J"}, second joules, {"Joules", , "Seconds"}}, QuantityTF]](Files/SchrodingerPDEComponent.zh/10.png) ,
,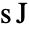 是薛定谔势,单位为
是薛定谔势,单位为 ![TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]](Files/SchrodingerPDEComponent.zh/12.png) .
.- 质量
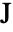 可以是各向同性、正交各向异性或各向异性的.
可以是各向同性、正交各向异性或各向异性的. 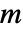 表示一个
表示一个  x
x 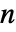 的矩阵,由下式给出:
的矩阵,由下式给出: - 对于磁场相互作用,SchrodingerPDEComponent 为:
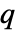 表示粒子的电荷,单位为哥伦布
表示粒子的电荷,单位为哥伦布 ![TemplateBox[{InterpretationBox[, 1], "C", coulombs, "Coulombs"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "C", coulombs, "Coulombs"}, QuantityTF]](Files/SchrodingerPDEComponent.zh/20.png) .
. 是磁矢势,单位为
是磁矢势,单位为 ![TemplateBox[{InterpretationBox[, 1], {"s", , "V", , "/", , "m"}, second volts per meter, {{(, {"Volts", , "Seconds"}, )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "V", , "/", , "m"}, second volts per meter, {{(, {"Volts", , "Seconds"}, )}, /, {(, "Meters", )}}}, QuantityTF]](Files/SchrodingerPDEComponent.zh/22.png) ,定义为
,定义为 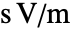 ,其中
,其中 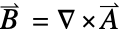 是磁通量密度,单位为
是磁通量密度,单位为 ![TemplateBox[{InterpretationBox[, 1], "T", teslas, "Teslas"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "T", teslas, "Teslas"}, QuantityTF]](Files/SchrodingerPDEComponent.zh/25.png) .
.- 薛定谔 PDE 项的单位为焦耳
![TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]](Files/SchrodingerPDEComponent.zh/26.png) 乘以波函数的单位,
乘以波函数的单位,![TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]/TemplateBox[{InterpretationBox[, 1], {{sqrt(, "m", )}}, square root meters, {sqrt(, "Meters", )}}, QuantityTF]^n TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]/TemplateBox[{InterpretationBox[, 1], {{sqrt(, "m", )}}, square root meters, {sqrt(, "Meters", )}}, QuantityTF]^n](Files/SchrodingerPDEComponent.zh/27.png) .
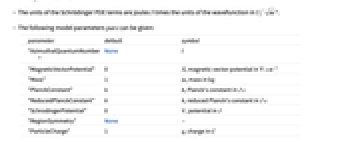
. - 可以给出以下模型参数 pars:
-
参数 默认值 符号 "AzimuthalQuantumNumber" None 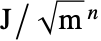
"MagneticVectorPotential" 0 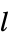 ,磁矢量势,单位为
,磁矢量势,单位为 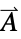
"Mass" 1 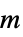 ,质量,单位为
,质量,单位为 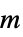
"PlanckConstant" 
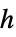 ,普朗克常数,单位为
,普朗克常数,单位为 
"ReducedPlanckConstant" 
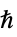 ,约化普朗克常数,单位为
,约化普朗克常数,单位为 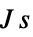
"SchrodingerPotential" 0 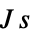
"RegionSymmetry" None 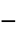
"ParticleCharge" 1  ,电荷,单位为
,电荷,单位为 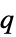
- 所有参数可能取决于
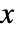 、
、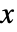 和
和  中的任何一个,以及其他因变量.
中的任何一个,以及其他因变量. - 带单位的参数将转换为国际单位制基本单位.
- 普朗克常数和简化普朗克常数的默认值采用国际单位制基本单位.
- 参数 "RegionSymmetry" 的一个可能选择为 "Axisymmetric".
- "Axisymmetric" 区域对称性表示截断柱坐标系,其中柱坐标通过去除角度变量而简化,如下所示:
-
维度 简化 通用方程 1D 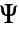
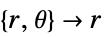
2D 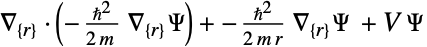
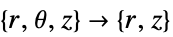
- 如果 "RegionSymmetry" 被设为 "Axisymmetric",则
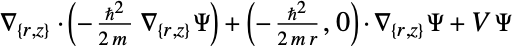 必须是各向同性的.
必须是各向同性的. - 对于 "AzimuthalQuantumNumber"
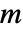 ,SchrodingerPDEComponent 为:
,SchrodingerPDEComponent 为: - 扩散分量影响 NeumannValue 的含义.
- 如果 SchrodingerPDEComponent 取决于在关联 pars 中指定为 …,keypi…,pivi,… 的参数
 ,则参数
,则参数 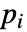 将替换为
将替换为  .
.
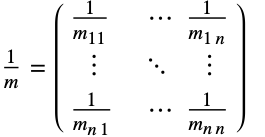
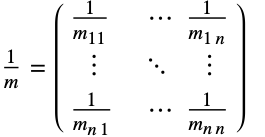
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (16)
一维 (6)
轴对称 (3)
应用 (12)
计算与时间无关的薛定谔偏微分方程算子的特征系统,普朗克常数为 1,质量为 1,势能为 ![]() :
:
找到具有约化普朗克常数 ![]() 和分段势能的 10 个最小特征值和特征函数,其中对于
和分段势能的 10 个最小特征值和特征函数,其中对于 ![]() 的负值,分段势能为
的负值,分段势能为 ![]() ,对于
,对于 ![]() 的正值,分段势能为
的正值,分段势能为 ![]() .
.
描述一个被限制在半径为 ![]() 的二维圆盘内的粒子,假设具有围绕通过圆盘中心的轴对称性. 假设粒子的波函数不依赖于极坐标.
的二维圆盘内的粒子,假设具有围绕通过圆盘中心的轴对称性. 假设粒子的波函数不依赖于极坐标.
考虑一个模型,其中波函数可以通过以下方式分离:![]() ,其中
,其中 ![]() 、
、![]() 和
和 ![]() 分别是圆柱坐标系中的径向、方位角和高度坐标. 这里,
分别是圆柱坐标系中的径向、方位角和高度坐标. 这里,![]() 是方位角量子数.
是方位角量子数.
这个特定示例考虑了一个被限制在具有无限势壁的环面内的粒子. 鉴于这些考虑,只需求解环面横截面中的 ![]() 即可.
即可.
创建一个辅助函数,使用偏微分方程算子找到不同方位角量子数值的六个特征态,假设在一个简化模型中,![]() 且
且 ![]() ,粒子在环面内的势能
,粒子在环面内的势能 ![]() :
:
可以探索不同方位角量子数值下能级如何变化. 为了举例说明这一点,计算 0 到 5 之间的 ![]() 的能量.
的能量.
观察到随着 ![]() 增大,能级呈非线性增长. 此外,可以注意到基态是非简并的,而第二和第三能级以及第四和第五能级是二重简并的.
增大,能级呈非线性增长. 此外,可以注意到基态是非简并的,而第二和第三能级以及第四和第五能级是二重简并的.
要探究方位量子数对波函数的影响,可以绘制总波函数 ![]() 的实部和虚部的图形. 为此,您可以选择任何
的实部和虚部的图形. 为此,您可以选择任何 ![]() 值,例如
值,例如 ![]() .
.
可以研究量子弹球系统,特别是一个被限制在二维布尼莫维奇体育场内的粒子.
将 Animate 应用于解:
将势能缩小 ![]() ,用 Animate 来绘制概率密度的动画:
,用 Animate 来绘制概率密度的动画:
建立一个带有约化普朗克常数和高斯势能 ![]() 的时间相关薛定谔偏微分方程算子:
的时间相关薛定谔偏微分方程算子:
可以对指向 ![]() 方向的磁场中的无自旋带电粒子进行建模. 粒子由初始波包描述,目标是研究磁场相互作用下概率密度的演化. 由于这是磁场中的带电粒子,因此可以预期其概率密度反映某种圆形轨迹,类似于经典带电粒子的行为. 因此,选择了非常高的磁通密度,使得回旋加速器半径达到埃的数量级.
方向的磁场中的无自旋带电粒子进行建模. 粒子由初始波包描述,目标是研究磁场相互作用下概率密度的演化. 由于这是磁场中的带电粒子,因此可以预期其概率密度反映某种圆形轨迹,类似于经典带电粒子的行为. 因此,选择了非常高的磁通密度,使得回旋加速器半径达到埃的数量级.
粒子的初始条件将由动量为 ![]() 的波包来描述,这意味着如果没有磁场相互作用,它将沿直线移动.
的波包来描述,这意味着如果没有磁场相互作用,它将沿直线移动.
由于长度单位为 Angstroms (![]() ),定义 PDE 算符时需要考虑到这一点. 因此, "ScaleUnits" -> {"Meters" -> "Angstroms"} 被用在 SchrodingerPDEComponent 的参数中.
),定义 PDE 算符时需要考虑到这一点. 因此, "ScaleUnits" -> {"Meters" -> "Angstroms"} 被用在 SchrodingerPDEComponent 的参数中.
使用 NeumannValue 求解透明边界条件的问题:
作为 Aharonov–Bohm 效应的演示,我们对在磁矢量势的影响下穿过两个狭缝的波包的散射过程进行了建模. 请注意,整个求解域的磁通密度为零,但磁矢量势却不然.
例如,域由两个狭缝和一个小孔定义,表示一个长螺线管,在其内部产生磁通密度,进而在整个域的其余部分产生磁矢量势场. 请注意,波函数不能与磁通密度非零的区域相互作用.
定义变量和参数,质量为非各向同性的,其值为有重空穴 (heavy hole) 的 ![]() (一种常见的半导体材料)的有效质量. 此处,"MagneticVectorPotential" 是磁通密度为
(一种常见的半导体材料)的有效质量. 此处,"MagneticVectorPotential" 是磁通密度为 ![]() ,半径为的
,半径为的 ![]() 的螺线管的参数,被转换为直角坐标.
的螺线管的参数,被转换为直角坐标.
请注意与没有磁场的情况相比,干涉图案是如何移动的,并且是不对称的.
属性和关系 (3)
检查各单位制之间扩散系数的差异. 计算普朗克常数除以电子质量:
下面的例子将显示在内部接口处自动应用 BenDaniel–Duke 边界条件.
考虑一个量子阱,宽度为 ![]() ,具有有限势
,具有有限势 ![]() ,波函数为
,波函数为 ![]() . 阱内粒子的质量为
. 阱内粒子的质量为 ![]() ,势垒区域中粒子的质量为
,势垒区域中粒子的质量为 ![]() . 因此,质量是位置
. 因此,质量是位置 ![]() 的函数. 量
的函数. 量 ![]() 和
和 ![]() 在势垒和阱相接的地方应该是连续的,在相接处应用 BenDaniel–Duke 边界条件. 事实上,将在相接处自动应用 BenDaniel–Duke 边界条件.
在势垒和阱相接的地方应该是连续的,在相接处应用 BenDaniel–Duke 边界条件. 事实上,将在相接处自动应用 BenDaniel–Duke 边界条件.
注意,阱域的长度 ![]() 单位是埃. 为了定义 PDE 算符,我们使用参数 "ScaleUnits"->{"Meters"->"Angstroms"}. 这会对模型其余的量进行转换,使得所有长度的单位都为埃. 这样也提高了数值解的质量.
单位是埃. 为了定义 PDE 算符,我们使用参数 "ScaleUnits"->{"Meters"->"Angstroms"}. 这会对模型其余的量进行转换,使得所有长度的单位都为埃. 这样也提高了数值解的质量.
从物理上讲,对于无穷远处的所有束缚态,波函数应该衰减直至变为 ![]() . 一种实用的建模方法是在外部边界处使用
. 一种实用的建模方法是在外部边界处使用 ![]() 的狄利克雷边界条件,该边界条件被放置在距量子阱中心足够远的地方. 在这种情况下,
的狄利克雷边界条件,该边界条件被放置在距量子阱中心足够远的地方. 在这种情况下,![]() 是非常合适的选择.
是非常合适的选择.
用 NDEigensystem 在细化网格上求解特征值问题:
特征值的单位是 ![]() ,鉴于单位米在参数中缩放为埃. 知道这一点后,特征值就可以转换为所需的能量单位.
,鉴于单位米在参数中缩放为埃. 知道这一点后,特征值就可以转换为所需的能量单位.
最后,可以比较用数值法和解析法所求得的能量特征值和概率密度.
以上表明,当采用 BenDaniel–Duke 边界条件时,NDEigensystem 给出的能量特征值在数值上与薛定谔方程的解析解相同. 此外,NDEigensystem 得到的波函数与解析解等效. 之所以如此,是因为数值法确保了波函数 ![]() 和量
和量 ![]() 的连续性.
的连续性.
巧妙范例 (1)
对于简化的薛定谔偏微分方程算子,设置变量和参数,质量和约化普朗克常数等于 ![]() :
:
使用 NDEigensystem 求解一维中与时间无关的薛定谔方程. 这个可视化的目的是看看势垒高度和势阱长度对本征态的影响. 你可以观察到增加势阱的长度会降低每个波函数的能量,而增加势垒高度会导致更高能量的本征值.
定义一个函数,来计算任何给定势垒高度、势阱宽度和本征态数量的本征态:
设置 Manipulate:
文本
Wolfram Research (2024),SchrodingerPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html (更新于 2024 年).
CMS
Wolfram 语言. 2024. "SchrodingerPDEComponent." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html.
APA
Wolfram 语言. (2024). SchrodingerPDEComponent. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html 年