SinDegrees

SinDegrees[θ]

gives the sine of degrees.

Details

  • SinDegrees and other trigonometric functions are studied in high-school geometry courses and are also used in many scientific disciplines.
  • The argument of SinDegrees is assumed to be in degrees.
  • SinDegrees is automatically evaluated when its argument is a simple rational multiple of 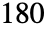; for more complicated rational multiples, FunctionExpand can sometimes be used.
  • SinDegrees of angle 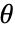is the ratio of the opposite side to the hypotenuse of a right triangle:
  • SinDegrees is related to CosDegrees by the Pythagorean identity TemplateBox[{theta}, SinDegrees]^2+TemplateBox[{theta}, CosDegrees]^2=1.
  • For certain special arguments, SinDegrees automatically evaluates to exact values.
  • SinDegrees can be evaluated to arbitrary numerical precision.
  • SinDegrees automatically threads over lists.
  • SinDegrees can be used with Interval, CenteredInterval and Around objects.
  • Mathematical function, suitable for both symbolic and numerical manipulation.

Examples

open allclose all

Basic Examples  (6)

The argument is given in degrees:

Calculate SinDegrees of 45 degrees for a right triangle with unit sides:

Calculate the sine by hand:

Verify the result:

Solve a trigonometric equation:

Solve a trigonometric inequality:

Plot over two periods:

Series expansion at 0:

Scope  (47)

Numerical Evaluation  (6)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

SinDegrees can take complex number inputs:

Evaluate SinDegrees efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Or compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix SinDegrees function using MatrixFunction:

Specific Values  (6)

Values of SinDegrees at fixed points:

SinDegrees has exact values at rational multiples of 30 degrees:

Values at infinity:

Simple exact values are generated automatically:

More complicated cases require explicit use of FunctionExpand:

Zeros of SinDegrees:

Extrema of SinDegrees:

Find the first positive maximum as a root of (dTemplateBox[{x}, SinDegrees])/(dx)=0:

Substitute in the result:

Visualize the result:

Visualization  (4)

Plot the SinDegrees function:

Plot over a subset of the complexes:

Plot the real part of SinDegrees:

Plot the imaginary part of SinDegrees:

Polar plot with SinDegrees:

Function Properties  (13)

SinDegrees is a periodic function with a period of 360 degrees:

Check this with FunctionPeriod:

SinDegrees is defined for all real and complex values:

SinDegrees achieves all real values between and :

The range for complex values is the whole plane:

SinDegrees is an odd function:

SinDegrees has the mirror property sin(TemplateBox[{z}, Conjugate])=TemplateBox[{{sin, (, z, )}}, Conjugate]:

SinDegrees is an analytic function of x:

SinDegrees is monotonic in a specific range:

SinDegrees is not injective:

SinDegrees is not surjective:

SinDegrees is neither non-negative nor non-positive:

SinDegrees has no singularities or discontinuities:

SinDegrees is neither convex nor concave:

SinDegrees is concave for x in [0,180]:

TraditionalForm formatting:

Differentiation  (3)

First derivative:

Higher derivatives:

Formula for the ^(th) derivative:

Integration  (3)

Compute the indefinite integral of SinDegrees via Integrate:

Definite integral of SinDegrees over a period is 0:

More integrals:

Series Expansions  (3)

Find the Taylor expansion using Series:

Plots of the first three approximations for SinDegrees around :

Fourier series:

SinDegrees can be applied to power series:

Function Identities and Simplifications  (5)

Double-angle formula using TrigExpand:

Angle sum formula:

Multiple‐angle expressions:

Recover the original expression using TrigReduce:

Convert sums to products using TrigFactor:

Convert to exponentials using TrigToExp:

Function Representations  (4)

Representation through CosDegrees:

The Pythagorean identity:

Representations through CosDegrees, TanDegrees and CotDegrees:

Representation through CscDegrees:

Applications  (22)

Basic Trigonomometric Applications  (3)

Given , find the SinDegrees of the angle :

Find the missing opposite side length of a right triangle with hypotenuse 5 given the angle is 30 degrees:

Draw a circle:

Trigonomometric Identities  (7)

Calculate the SinDegrees value of 105 degrees using the sum and difference formulas:

Compare with the result of direct calculation:

Calculate the SinDegrees value of 15 degrees using the half-angle formula :

Compare this result with directly calculated SinDegrees:

Calculate the product of two SinDegrees using the trigonometric product to sum formula :

Compare this result with directly calculated product of two SinDegrees instances:

Simplify trigonometric expressions:

Verify trigonometric identities:

Use the law of sines to find the length of the side opposite to the angle angle, given the length of the side and :

This could be calculated via the formula :

The numerical value of :

Calculate the base length of an isosceles triangle given the leg length and the vertex angle :

Calculate the base:

Get the numerical value of the base:

Trigonomometric Equations  (2)

Solve a basic trigonometric equation:

Solve trigonometric equations including other trigonometric functions:

Solve trigonometric equations with conditions:

Trigonomometric Inequalities  (2)

Solve this trigonometric inequality:

Solve this trigonometric inequality including other trigonometric functions:

Advanced Applications  (8)

Lissajous figure:

Equiangular (logarithmic) spiral:

Plot a sphere:

Plot a torus:

Plot waves:

Approximate the almost nowhere differentiable Riemann–Weierstrass function:

Intensity of the Fraunhofer diffraction pattern of a circular aperture versus diffraction angle:

Find a point on a unit circle using CosDegrees and SinDegrees functions:

Properties & Relations  (11)

Check that 1 degree is radians:

Basic parity and periodicity properties are automatically applied:

Complicated expressions containing trigonometric functions do not simplify automatically:

Another example:

Use FunctionExpand to express SinDegrees in terms of radicals:

Compositions with the inverse trigonometric functions:

Solve a trigonometric equation:

Numerically find a root of a transcendental equation:

Plot the function to check if the solution is correct:

The zeros of SinDegrees:

FunctionExpand applied to SinDegrees generates expressions in trigonometric functions in radians:

ExpToTrig applied to the outputs of TrigToExp will generate trigonometric functions in radians:

SinDegrees is a numeric function:

Possible Issues  (1)

Machine-precision input is insufficient to get a correct answer:

With exact input, the answer is correct:

Neat Examples  (5)

Trigonometric functions are ratios that relate the angle measures of a right triangle to the lengths of its sides:

Solve a trigonometric equation:

Add some condition to the solution:

Some arguments can be expressed as a finite sequence of nested radicals:

Indefinite integral of :

Noncommensurate waves (quasiperiodic function):

Wolfram Research (2024), SinDegrees, Wolfram Language function, https://reference.wolfram.com/language/ref/SinDegrees.html.

Text

Wolfram Research (2024), SinDegrees, Wolfram Language function, https://reference.wolfram.com/language/ref/SinDegrees.html.

CMS

Wolfram Language. 2024. "SinDegrees." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SinDegrees.html.

APA

Wolfram Language. (2024). SinDegrees. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SinDegrees.html

BibTeX

@misc{reference.wolfram_2024_sindegrees, author="Wolfram Research", title="{SinDegrees}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/SinDegrees.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sindegrees, organization={Wolfram Research}, title={SinDegrees}, year={2024}, url={https://reference.wolfram.com/language/ref/SinDegrees.html}, note=[Accessed: 17-November-2024 ]}